Inscription / Connexion Nouveau Sujet
Impédance à calculer
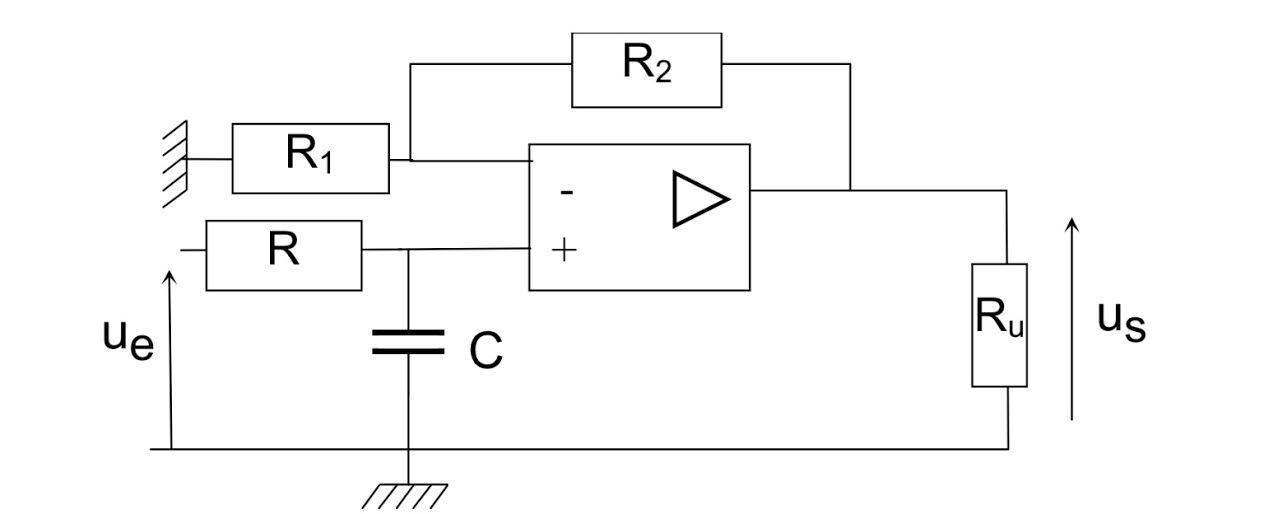
Bonjour, je n'arrive pas à calculer l'impédance d'entrée ainsi que la fonction de transfert du circuit ci-joint :
Le circuit est alimenté par une tension sinusoïdale u_e.
Merci pour votre aide !
Bonjour
Les courants d'entrée dans l'ampli op sont totalement négligeables. Le courant d'entrée traverse donc R et C qui apparaissent ainsi en série. Cela devrait te permettre d'obtenir l'impédance de sortie.
Pour la suite : l'ampli op ( ALI) fonctionne a priori en régime linéaire. Exprime donc V+ en fonction de Ue et des impédances complexes ; exprime V- en fonction de Us, R1 et R2. Il suffit ensuite d'écrire V+ = V- pour obtenir la fonction de transfert.
Je te laisse réfléchir à cela et proposer une solution.
Bonjour
Pour le premier point, je dois calculer l'impedance d'entrée en fait pas de sortie.,. Mais si j'ai compris ce que tu me dis, je dois simplement chercher la résistance équivalente de R et C, non ?
Pour la fonction de transfert, j'envisage d'appliquer la loi de Millman aux différents noeuds :
Au point V+ je dirais : u_e(1/R + jCw)
Et en V- j'aurai u_s(1/R1 + 1/R2) mais qu'en est-il de Ru ?
Je suis un peu perdu !
Je suis un peu perdu !
Tu as eu un cours sur l'ampli op (ALI) ? Si oui, commence par bien l'étudier. Je peux tout de même t'aider.
1° Puisque le courant entrant dans l'ampli op par l'entrée + (non inverseuse) est d'intensité totalement négligeable, le générateur non représenté sur le schéma chargé de créer la tension d'entrée fournit le même courant que s'il était branché seulement aux bornes de l'association série {R,C}. L'impédance d'entrée est donc la somme R+Zc
Pour V-, l'application du théorème de Millman est possible mais la notion de diviseur de tension est plus rapide puisque, comme déjà dit, la branche R et la branche C sont parcourues par le même courant.
Pour V+, l'application du théorème de Millman est une bonne idée même si, pour un cas aussi simple, d'autres méthodes sont possibles.
mais qu'en est-il de Ru ?
Tant que le courant sortant de l'ampli op reste d'intensité efficace inférieure à environ 20mA (cette valeur dépend des modèles d'ampli op), la sortie de l'ampli op se comporte en générateur idéal de tension : elle fournit une tension de sortie indépendant de l'intensité de sortie . On peut donc considérer Us comme indépendant de la valeur de Ru sous réserve que cette valeur de Ru ne soit pas trop faible. Cette hypothèse est, par défaut, considérée comme vérifiée même si elle n'est pas rappelée dans tous les énoncés d'exercices. Bref : l'expression de la fonction de transfert ne va pas dépendre de Ru.
Du coup est ce que les résultats sont corrects pour ce que j'ai écrit en V+ et V- ?
Non !
Plus gênant : tu proposes des expressions qui ne sont pas homogènes : une tension ne peut pas être le produit d'une autre tension par une admittance ou une conductance. Une tension peut en revanche être le produit d'une tension par une grandeur sans dimension, cette grandeur sans dimension pouvant être le rapport de deux résistances...
Je te fournis les résultats ; essaie de bien comprendre et pose des questions si tu le juges utile. Ensuite, tu devrais être capable d'obtenir l'expression de la fonction de transfert.
Impédance d'entrée :
L'association série {R,C} se comporte en diviseur de la tension d'entrée, le potentiel de l'entrée non inverseuse étant ainsi :
Le théorème de Millman appliqué à l'entrée inverseuse conduit à :
Je te laisse continuer... Tu devrais obtenir la fonction de transfert d'un classique passe-bas du premier ordre...
Millman si on veut ... mais on peut tout aussi bien s'en passer.
Comme le courant est négligeable dans l'entrée de l'ampli, on a, pour calculer V-, le schéma équivalent suivant:

C'est donc un simple diviseur de tension --> V- = Us * R1/(R1+R2)

Soit Ro la résistance interne de sortie de l'ampli et A le gain en tension de l'ampli. (Au point de fonctionnement considéré).

i2 = e * (1 - R1/(R1+R2))/R2
i2 = e/(R1+R2)
i1 = [-A * e * R1/(R1+R2) - e]/Ro
i1 = - e * (A.R1 + R1 + R2)/(Ro.(R1 + R2))
i = i1 - i2
i = - e * (A.R1 + R1 + R2)/(Ro.(R1 + R2)) - e/(R1+R2)
i = - e/(R1+R2) * [1 + (A.R1 + R1 + R2)/Ro]
i = - e(Ro + A.R1 + R1 + R2)/(Ro.(R1+R2))
Rs = -e/i
Rs = Ro.(R1+R2)/(A.R1 + R1 + R2 + Ro)
Sauf distraction. 
Bonjour Touker
Comme expliqué dès le début dans mon message du 16-08-17 à 19:29 :
Pour V+, l'application du théorème de Millman est une bonne idée même si, pour un cas aussi simple, d'autres méthodes sont possibles.
Par contre je ne comprends pas comment tu utilises Millman
La méthode de Millman consiste très simplement à raisonner sur les intensités puis à remplacer chaque intensité par son expression en fonction de la différence de potentiels et de la résistance ou impédance. Ici, il suffit de remarquer que les deux résistances sont parcouru par un courant de même intensité puisque le courant d'entrée dans l'ampli op est d'intensité négligeable : en choisissant comme sens conventionnel du courant le sens gauche-droite du schéma pour les deux résistances :
Puisque par convention, le potentiel de la masse est choisi nul, le regroupement des termes dépendant de V- conduit à :
Ce qui te donne très simplement l'expression déjà fournie. De façon plus générale, il suffit d'appliquer la loi des nœuds puis de remplacer chaque intensité par son expression en fonction de la différence de potentiel et de la résistance ou impédance. Tu trouveras plus d'explications et quelques applications simples sur la fiche n°1 que tu trouveras ici :
Pour l'impédance de sortie, dans la mesure où l'ampli op est idéal, les explications que je t'ai fournies dans mon message du 16-08-17 à 19:29 sont valides. La sortie de l'ampli op se comporte vis à vis de Ru comme un générateur de tension idéal donc un générateur de tension de résistance de sortie nulle.
Re,
C'est bon pour la fonction de transfert bien caractéristique d'un passe bas d'ordre 1
H= ((R1+R2)/R1)/(1+jCRw) 


