Inscription / Connexion Nouveau Sujet
impédance
bonjour excusez moi je tentes de trouver une fonction de transfert du premier ordre
e sais que c'est un filtre passe bas donc je devrais avoir Ho\1+j(w\wo)
mais quand je n'arrive pas à retrouver cette formule (alpha est un reel fixé)
quand je fais un pont diviseur de tension avec z(équivalent) je trouve
1\(1+alpha+alpha*RJCW) je ne sais pas si c'est bon et comment la metresous la mettre indiqué ci-dessus pouvez-vous l'aider svp ?
c'est à propos du circuit suivant: 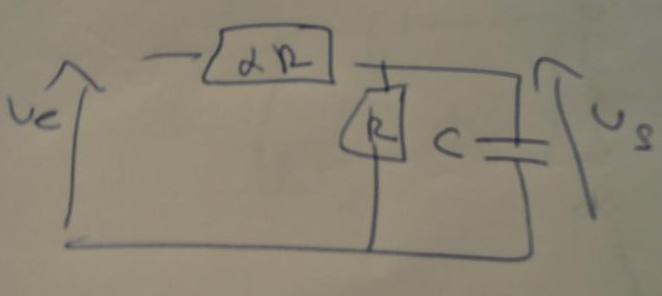
***Image recadrée***
C'est bon (avec j au lieu de J)
Us/Ue = 1/((1+alpha) + jwRC.alpha)
et en divisant numérateur et dénominateur par (1 + alpha), il vient :
Us/Ue = (1/(1+alpha))/(1 + jw.(alpha/(1+alpha))RC)
--> Ho = 1/(1+alpha)
et 1/wo = (alpha/(1+alpha)).RC
wo = ((1+alpha)/alpha)/(RC)
Sauf distraction.

bonjour, en fait Ho représente le gain pur ?
Si alpha=1 pour le diagramme de bode en amplitude je trouve
x<<1 Gdb=20log(1/2)
x>>1 Gdb= 2àlog(1/2)-10log(x)
est-ce exact svp ?
si je calcule l'impédance d'entrée je sais que
Ze=Ue/Ie=
est ce que je peux remplacer Ue par Us*H ?
H(w) = Ho/(1+j(w/wo))
|H| = Ho/RCarrée(1 + (w/wo)²)
G = 20.log|H|
G = 20.log(Ho) - 10.log(1 + (w/wo)²)
Diagramme asymptotique :
- Pour w petit devant wo , on a G = 20.log(Ho)
- Pour w grand devant wo , on a G = 20.log(Ho) - 20.log(w/wo)
-----
Z entrée = alpha.R + (R // 1/(jwC)) = ...
-----
Sauf distraction. 
bonjour et joyeux noel
mais si je trouve 20 log(1/2) sur le diagramme de bode où l'axe des abscisses est caractérisée par log(X), 20 log(1/2) se situe au dessus ou en dessous de l'axe des abscisses svp ?
et comment trouvez-vous Z entrée svp ?
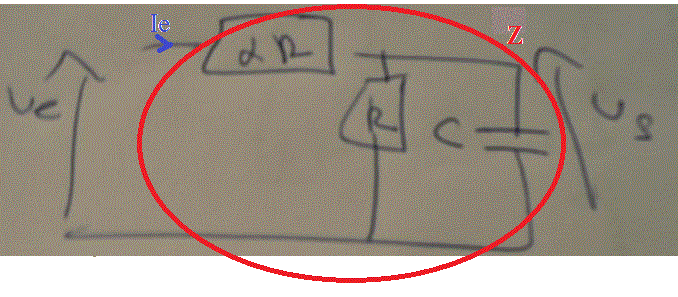
Ze = Ue/Ie
Et on voit sur le schéma que Ze correspond au Z que j'ai entouré en rouge.
Soit donc (alpha*R) en série avec (R en parallèle sur C)
Z entrée = alpha.R + (R // 1/(jwC)) = ...
Sauf distraction 


