Niveau licence

Hydrostatique : plan incliné et forme de la surface

Posté par
nico045 15-10-16 à 16:29

Bonjour,

J'ai fait l'exercice suivant et je voulais savoir si ce que j'ai fait était juste :
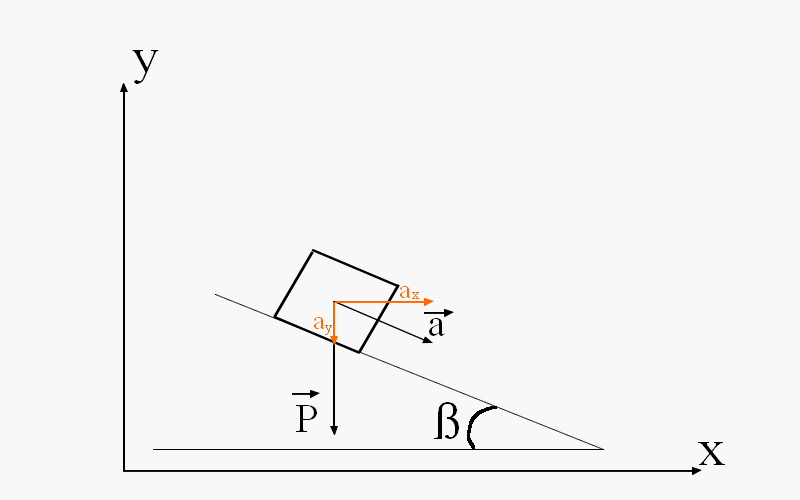
Hydrostatique : plan incliné et forme de la surface

On considère un récipient contenant de l'eau qui se déplace sur un plan incliné d'angle $\beta$ et avec une accélération a. On cherche à déterminer la forme de la surface de l'eau.

Pour cela on sait qu'à la surface le potentiel est constant, par conséquent on doit avoir :

U = gy + a.x = U₀ x = x i + y j (vecteur position)

avec a = a_x i + - a_y j

le produit scalaire a.x = $a_x \cdot x sin(\beta) - a_y \cdot y cos(\beta)$

$U_0 = y(g -a_y cos(\beta) ) + x a_x sin(\beta)$

$y = \frac { U_0} {g -a_y cos(\beta)} - \frac { x a_x sin(\beta)} {g -a_y cos(\beta)}$

Ce qui donnerait finalement $y = C_1 - x*C_2$
cependant pour tracer l'allure de la courbe j'ai des problèmes puisque les constantes peuvent être positives ou négatives suivant la valeur de $\beta$ .

Y a-t-il une erreur quelque part ?

Posté par re : Hydrostatique : plan incliné et forme de la surface 15-10-16 à 19:29

Bonsoir
Je note "a" la norme du vecteur accélération.
Dans le référentiel lié au récipient, chaque goutte d'eau (masse élémentaire dm d'eau) est soumises aux forces de pressions, à son poids et à la pseudo force d'inertie d'entraînement $\overrightarrow{dF_{i}}=-dm.\overrightarrow{a}$ . Tout se passe comme si l'eau était immobile dans le champ de pesanteur apparent :

$\overrightarrow{g_{a}}=\overrightarrow{g}-\overrightarrow{a}=-a.\cos\left(\beta\right).\overrightarrow{i}-\left(g-a.\sin\left(\beta\right)\right).\overrightarrow{j}$
La surface d'eau à l'équilibre est alors une surface plane perpendiculaire à la direction du vecteur g_a, direction que l'on pourrait matérialiser par un fil à plomb lié au récipient. Ce fil à plomb appartiendrait au plan (Oxy), il serait incliné vers l'arrière, sa direction faisant avec la verticale (Oy) un angle tel que :

$\tan\left(\alpha\right)=\frac{a.\cos\left(\beta\right)}{g-a.\sin\left(\beta\right)}$
La valeur maximale de a est obtenue en absence de frottement entre le plan incliné et le récipient :

$a_{max}=g.\sin\left(\beta\right)$
Ce cas limite correspond à une valeur maximale de vérifiant :

$\tan\left(\alpha_{max}\right)=\frac{g.\sin\left(\beta\right).\cos\left(\beta\right)}{g-g.\sin^{2}\left(\beta\right)}=\tan\left(\beta\right)\quad soit\quad\alpha_{max}=\beta$
Ce cas limite correspond à un fil à plomb perpendiculaire au plan incliné, donc à une surface libre de l'eau parallèle au plan incliné.
Cependant, la méthode des surfaces équipotentielles doit être connue : elle est indispensable dans des cas plus compliqués. Si on note U le potentiel, on obtient :

$\overrightarrow{grad}\left(U\right)=-\overrightarrow{g_{a}}=a.\cos\left(\beta\right).\overrightarrow{i}+\left(g-a.\sin\left(\beta\right)\right).\overrightarrow{j}$
En projetant d'expression sur les deux axes, on obtient :

$\begin{cases} \\ \frac{\partial U}{\partial x}=a.\cos\left(\beta\right)\\ \\ \frac{\partial U}{\partial y}=g-a.\sin\left(\beta\right) \\ \end{cases}$
Cela conduit à :
$U=a.\cos\left(\beta\right).x+\left[g-a.\sin\left(\beta\right)\right]y+constante$
Les équations des plans isopotentiels sont de la forme :

$y=\frac{a.\cos\left(\beta\right)}{g-a.\sin\left(\beta\right)}\cdot x+C$
Cela conduit aux mêmes conclusions...

Posté par re : Hydrostatique : plan incliné et forme de la surface 15-10-16 à 23:00

J'ai commis une erreur de signe en passant de l'avant dernière formule à la dernière : Il faut lire que les plans équipotentiels ont pour équations :

$y=-\frac{a.\cos\left(\beta\right)}{g-a.\sin\left(\beta\right)}\cdot x+C$
ce qui, dans le cas limite de l'absence de frottement entre le récipient et le plan incliné conduit à :
$y=-\tan\left(\beta\right)\cdot x+C$
la surface libre de l'eau est bien ainsi parallèle au plan incliné.

Posté par re : Hydrostatique : plan incliné et forme de la surface 16-10-16 à 11:56

Merci pour cette explication rigoureuse, cela m'a permis d'éclaircir certains points.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Hydrostatique : plan incliné et forme de la surface

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique