Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Hodographe et trajectoire

Posté par
Samuel7 10-04-21 à 19:23

Bonjour,
J'aimerais avoir de l'aide sur l'exercice suivant:

Par rapport à un repère R(O,\vec{u_{x}},\vec{u_{y}},\vec{u_{z}}) , un point P effectue un mouvement dont l'hodographe de pôle O a pour équation :

\left\lbrace\begin{matrix}\dot{x}^{2}+\dot{y}^{2}-4=0 \\ \dot{z}^{2}=0 \end{matrix}\right.

1. Identifier l'hodographe
a. Quelle conclusion en tire-t-on sur la nature du mouvement ?
b. Préciser les directions des vecteurs \vec{v}(𝑃/𝑅) et accélération \vec{a}(𝑃/𝑅) par rapport à l'hodographe et celle de \vec{a}
(𝑃(/𝑅) par rapport à  la trajectoire.
2. On paramètre l'équation de la trajectoire de P en posant : x=\sqrt{2}cos\theta 𝑎𝑣𝑒𝑐 \dot{\theta }=\frac{2}{\sqrt{1+sin^{2}\theta }}

Sachant que pour 𝜃 = 0, 𝑦 = 0 et 𝑧 = 0
a. De terminer l'équation cartésienne de la trajectoire et identifier celle-ci.
b. Calculer le rayon de courbure de la trajectoire et identifier celle-ci.
c. Donner sa valeur pour 𝜃 = 0.

Voilà

Au 1) je ne sais pas exactement ce qu'on me demande par identifier l'hodographe mais je propose que l'hodographe soit un cercle de centre l'origine du repère et de rayon 2 en voyant la première équation du système et vu aussi que z est constant.

a) Je dirai que le mouvement est circulaire puisque l'hodographe est aussi un cercle.
b)je n'ai pas vraiment d'idée.

2) Comment procéder?

Merci d'avance.

Posté par
vanoisere : Hodographe et trajectoire 10-04-21 à 19:36

Bonsoir
OK pour le cercle mais on peut en dire plus concernant le vecteur vitesse et le vecteur accélération.

Posté par
Samuel7re : Hodographe et trajectoire 10-04-21 à 19:44

Les vecteurs vitesse et accélération ont la même direction par rapport à  l'hodographe?!
Je sais juste que l'hodographe est le lieu des points P tels qu'à chaque instant t \vec{OP}(t)=\vec{v}(t) donc \vec{OP}et\vec{v} ont la même direction. Or le vecteur accélération est équipollent au vecteur vitesse sur l'hodographe donc ils ont la même direction

Posté par
vanoisere : Hodographe et trajectoire 10-04-21 à 19:57

Que peux-tu dire de la norme du vecteur vitesse ? Dans ces conditions, que peut-on dire du vecteur accélération sachant que le mouvement est plan ?

Posté par
Samuel7re : Hodographe et trajectoire 10-04-21 à 20:15

Ah! Je dirai que la norme du vecteur vitesse vaut 2 puisque l'équation de l'hodographe est celle de la vitesse aussi et \sqrt{\dot{x}^{2}+\dot{y}^{2}}=2
La vitesse est constante donc l'accélération est nulle

Posté par
Samuel7re : Hodographe et trajectoire 10-04-21 à 20:18

Mais rien ne me dit que la vitesse est constante. Je retire ma deuxième phrase de la réponse ci-dessus.  Je ne sais pas quoi conclure.

Posté par
vanoisere : Hodographe et trajectoire 10-04-21 à 21:34

Citation :
La vitesse est constante donc l'accélération est nulle

Cette phrase est effectivement fausse en parlant des vecteurs vitesse et accélération. Pourtant, tu viens de démontrer que la norme du vecteur vitesse est une constante... Alors ? Réfléchis et essaie de répondre aux questions posées de façon précise.

Posté par
Samuel7re : Hodographe et trajectoire 12-04-21 à 11:48

Bonjour,
1)a)Le mouvement est circulaire puisque l'hodographe est aussi un cercle. De plus, la vitesse est constante donc le mouvement de P est circulaire uniforme.

b)Le vecteur vitesse est tangentielle par rapport à la trajectoire donc le vecteur vitesse est normale par rapport à l'hodographe.
Le vecteur accélératon est équipollent au vecteur vitesse du point P' de l'hodographe donc le vecteur accélération est tangentielle par rapport à l'hodographe.
La dérivée de la vitesse par rapport au temps est nulle donc le vecteur accélération est normale par rapport à la trajectoire de P.

Posté par
vanoisere : Hodographe et trajectoire 12-04-21 à 12:01

Pas mal de choses à revoir par rapport à ton dernier message. A lire l'historique des messages que tu as déjà postés, il me semble bien que l'expression de l'accélération dans la base de Frenet  soit connue. Je reprends point par point :

Citation :
Le mouvement est circulaire puisque l'hodographe est aussi un cercle

Faux !  Rien ne permet d'affirmer cela ! En revanche, tu peux dire que le mouvement est uniforme  puisque la norme du vecteur vitesse reste constante. Cependant, le vecteur vitesse varie au cours du temps car sa direction et son sens varient. Le vecteur accélération n'est donc pas le vecteur nul.
Citation :
donc le vecteur accélération est tangentielle par rapport à l'hodographe.

Cela est faux dans le cas général. Cependant : reprend l'expression de l'accélération dans la base de Frenet. Puisque la norme du vecteur vitesse est constante, l'accélération tangentielle est le vecteur nul. Reste donc l'accélération normale qui, effectivement est orthogonale au vecteur vitesse et orienté vers le centre de courbure de la trajectoire qui, ici, n'est pas un cercle. Ta dernière phrase est donc correcte.
Je te laisse continuer...

Posté par
Samuel7re : Hodographe et trajectoire 12-04-21 à 12:04

Je tente le 2)a)
x=\sqrt{2}cos\theta. Lorsque je dérive x et que je résouds la première équation en \dot{y} pour enfin retrouver l'expression de y je trouve y=\sqrt{2}sin\theta
j'ai donc y=\frac{cos\theta sin\theta }{x}
.  Est-ce bien ce qu'on me demande?

Posté par
Samuel7re : Hodographe et trajectoire 12-04-21 à 12:24

vanoise @ 12-04-2021 à 12:01


Cela est faux dans le cas général.

Que peut-on dire alors du vecteur accélération par rapport à l'hodographe?

Posté par
vanoisere : Hodographe et trajectoire 12-04-21 à 12:52

Citation :
Que peut-on dire alors du vecteur accélération par rapport à l'hodographe?

Rien de spécial dans le cas le plus général où ni l'accélération tangentielle ni l'accélération normale ne sont nulles.
Pas d'accord avec ton message de 12h04 : tu utilises le fait que le mouvement est circulaire et uniforme. Cela est faux : un mouvement circulaire uniforme conduirait à  \dot{\theta}=constante alors que cette grandeur dépend de .
En dérivant l'expression de x en fonction de par rapport au temps, tu obtiens \dot{x} en fonction de \dot{\theta} et de \theta  puis seulement en fonction \theta puisque l'expression de \dot{\theta} en fonction de \theta est fournie.

L'équation de l'hodographe va alors te permettre d'obtenir \dot{y}^{2} puis par intégration l'expression de y.

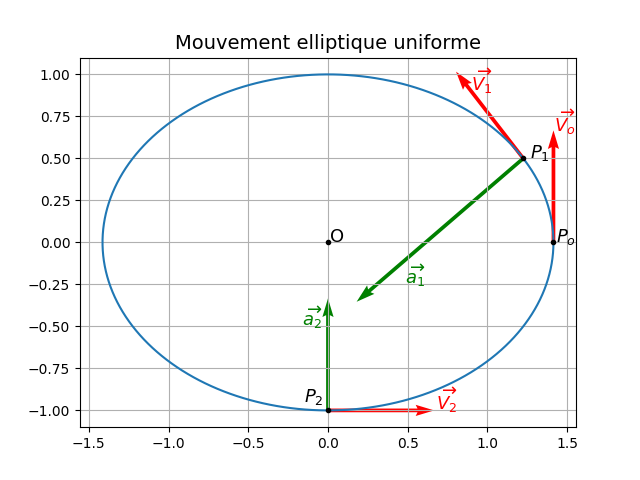
Voici une illustration graphique de cet exercice qui pourra t'aider et même , au poins partiellement, t'auto-corriger.

Hodographe et trajectoire

Posté par
Samuel7re : Hodographe et trajectoire 12-04-21 à 22:42

En suivant vos indications je trouve
y=sin.
x²=2cos²
    =2(1-sin²)
...
y²+½(x²)=1 est l'équation de la trajectoire.
La trajectoire est un ellipse de demi-grand axe √2 et de demi-petit axe 1.

b) Après dérivation j'obtiens
\ddot{x}=-2\dot{\theta}²sin²\theta
\ddot{y}=-\dot{\theta}²sin\theta
J'ai calculé la norme de l'accélération puis posé l'égalité entre cette norme et (v²)/Rc, Rc étant le rayon de courbure.
J'obtiens Rc=(√(1+sin²))/sin.

Au c) la valeur n'existe pas

Prière vérifier. Désolé pour le fait que je n'ai pas détaillé mes calculs. J'écris sur mon phone et je n'y suis pas à l'aise.

Posté par
vanoisere : Hodographe et trajectoire 13-04-21 à 11:42

D'accord avec ton équation de trajectoire. Petite remarque : puisque l'énoncé ne fournit de renseignements que sur les carrés des composantes du vecteur vitesse, on aurait pu poser :

\dot{y}=-\sqrt{4-\dot{x}^{2}} , ce qui aurait conduit à y=-sin(). Cela revient à inverser le sens de rotation sur l'ellipse. Cette imprécision de l'énoncé n'est pas bien grave dans la mesure où toutes les réponses demandées sont indépendantes du sens de rotation.

Concernant le rayon de courbure : ton résultat n'est pas réaliste : le rayon de courbure doit être minimum pour =0 et = et maximum pour =/2 et =3/2 sans jamais être ni nul ni infini.

Je n'ai pas le détail de ton calcul (effectivement : pas facile d'utiliser l'éditeur d'équations avec un téléphone...) mais peut-être as-tu considéré \ddot{\theta} comme une valeur nulle alors que \dot{\theta} dépend de donc de t... Je t'explique la méthode pour la composante de l'accélération sur x :

x=\sqrt{2}.\cos\theta\quad donc\quad\dot{x}=-\sqrt{2}.\dot{\theta}.\sin\left(\theta\right)=-2\sqrt{2}\cdot\dfrac{\sin\left(\theta\right)}{\sqrt{1+\sin^{2}\left(\theta\right)}}

\ddot{x}=-2\sqrt{2}.\dot{\theta}\cdot\dfrac{d\left(\dfrac{\sin\left(\theta\right)}{\sqrt{1+\sin^{2}\left(\theta\right)}}\right)}{d\theta}=-\dfrac{4\sqrt{2}}{\sqrt{1+\sin^{2}\left(\theta\right)}}\cdot\dfrac{d\left(\dfrac{\sin\left(\theta\right)}{\sqrt{1+\sin^{2}\left(\theta\right)}}\right)}{d\theta}

Je te laisse continuer...

Posté par
Samuel7re : Hodographe et trajectoire 13-04-21 à 22:38

Bonsoirvanoise,
Effectivement je considérais à tort \ddot{\theta } comme une valeur nulle. J'ai pu terminer l'exercice.
Merci pour votre aide !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !