Inscription / Connexion Nouveau Sujet
Hélicoptère et hélices
bonjour,
je suis entrain de faire un exercice de mécanique cependant je bloque sur la question 2, car j'ai un expression de vitesse trop compliquée, me bloquant pour la suite
Enoncé :
On considère un hélicoptère se déplaçant horizontalement en ligne droite. Le point A, centre de l'hélicoptère auquel est associé la masse de l'objet, s'éloigne alors de l'origine O du repère cartésien et est repéré par son abscisse x. On suppose que le point M, à l'extrémité d'une pale, décrit une trajectoire circulaire
uniforme de centre A et de rayon R dans la référentiel (A,i,j,k ).
1) Exprimer le vecteur position OM dans le référentiel R=(O,i,j,k ) en introduisant la base local u(r) u(
)
des coordonnées polaires au point M
2) En déduire l'expression du vecteur vitesse du point M.
3)A quelle condition sur les vecteurs i et u() la vitesse du point M est-elle maximale ? Pour quel
angle θ cette condition est-elle réalisée ?
Bonjour,
plusieurs méthodes, plus ou moins simples, peuvent être utilisées pour résoudre ce problème. As-tu étudié en cours la "composition des vitesses" et "la composition des accélérations ? Entre autres choses : la notion de vitesse relative et la notion de vitesse d'entraînement te sont-elles familières ?
OK ! On peut s'en passer dans ce problème simple. Les précisions ci-dessous devraient t'aider.
Puisque R est une distance fixe au cours du temps et en orientant correctement le vecteur :
La valeur de la vitesse est la norme du vecteur vitesse :
je viens de comprendre mon erreur merci
donc
pour la suite de l'exercice :
2) En déduire l'expression du vecteur vitesse du point M.
3)A quelle condition sur les vecteurs i et u() la vitesse du point M est-elle maximale ? Pour quel
angle θ cette condition est-elle réalisée ?
4) En déduire la vitesse maximale d'avancement de l'hélicoptère selon l'axe ( O , i ) sachant que la vitesse du point M doit être inférieure à la vitesse du son v(son) en tout instant.
La vitesse est effectivement maximale lorsque les vecteurs 
et sont colinéaires et de même sens. Je ne vois pas bien clairement l'orientation de ton angle
sur ton schéma mais a priori la vitesse est maximale pour =3
/4 rad. Je ne vois pas l'intérêt de ton calcul sur ce point !
Pour la dernière question, la valeur de est-elle fournie ?
l'angle est orienté dans le sens trigonométrique
je ne vois pas pourquoi =3/4 rad
non aucunes valeurs de ou de la dérivé de ne sont données
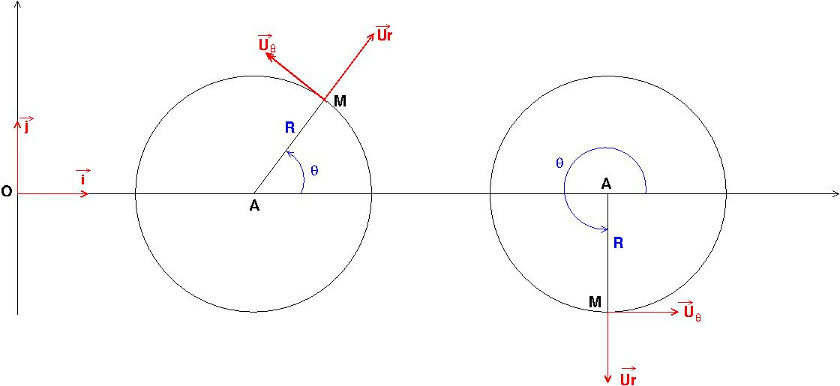
Voici un schéma qui devrait t'aider : à gauche : position quelconque ; à droite, cas où les vecteurs et sont colinéaires.
Pour la dernière question, il faut :
où VS désigne la vitesse du son.
Bonjour à vous deux,
@ masterred : merci de recopier intégralement les éléments que tu postes ici (hormis les images, voire les énoncés de concours de plusieurs pages).
Pour cette fois, je laisse ton message du 12-03-16 à 15:42. La prochaine fois, je n'aurais pas de scrupule à supprimer ta démonstration manuscrite et scannée.
Merci.
Annuler
connectez vous