Inscription / Connexion Nouveau Sujet
Hauteur atteinte
Salut à tous , encore moi .
J'ai besoin d'aide .
Merci d'avance .
Un enfant lance une boule avec la vitesse V0 de valeur 4m/s , dans le champ de pesanteur uniforme g=10N/kg .Au moment du lancé , la boule se situe à 1,8 m au -dessus du sol dans la main de l'élève.
Déterminer la hauteur atteinte par la boule par rapport au sol avant de redescendre .
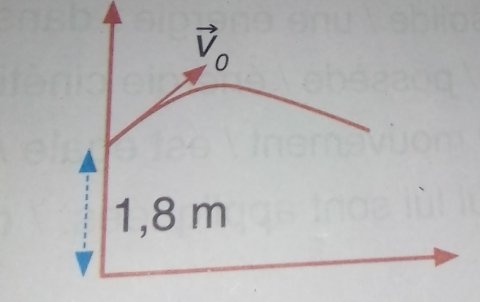
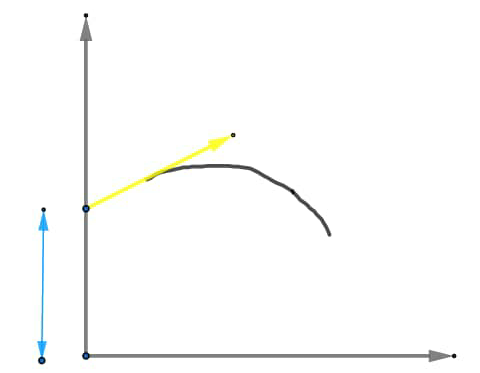
J'ai pu faire un schéma de la situation .
NB: la distance en bleue représente la distance de 1,8m ;
Le vecteur en jaune est le vecteur V0 .
Salut,
Je pense qu'il faut utiliser le fait qu'en absence de frottement, l'énergie mécanique se conserve. On peut ainsi noté Em(A)=Em(B) avec A la position initiale et B la position où la boule atteint la hauteur maximale. Une petite question intermédiaire qui pourrait t'aider, que vaut l'énergie cinétique Ec(B) ?
C'est la formule générale en effet. Cependant, tu peux en dire plus, lorsque la boule atteint sa hauteur maximale, la hauteur avant de redescendre, la vitesse est nulle. Si elle ne serait pas nulle cela voudrait dire que la boule continue de monter et donc ce n'est pas la hauteur maximale. Ainsi, Ec(B)=0. Je commence le calcul, je te laisse finir:
Em(A)=Em(B)
Ec(A)+Epp(A)=Epp(B)
Bonjour à vous deux,
Très bonne initiative lseioz d'aider à son tour tout en recevant également de l'aide 
Une autre alternative, abordée en terminale c'est d'appliquer la deuxième loi de Newton (en considérant également qu'il n'y a pas de frottement fluide, ni de poussée d'Archimède appliquée au système). Il y a une fiche intitulée "mouvement d'un projectile".

Bonjour,
Juste une remarque en passant ....
@Iseioz
Ce que tu dis de la vitesse de la boule quand elle atteint le sommet de la trajectoire n'est vrai que si la boule est lancée verticalement.
Le schéma posté par Othniel2 évoque une vitesse initiale oblique.
Bonjour à tous,
Oui c'est vrai...
Je me rappelle qu'en première on faisait des exercices de ce style en utilisant la conservation de l'énergie mécanique.
OK odbugt1 et si on utilisait
la variation de l'énergie cinétique qui est égale à la somme des travaux des forces extérieures en considérant que la vitesse finale est nulle au moment où l'objet redescend ?
On ne précise pas une valeur de l'angle avec lequel est lancée la balle ?
Mon intervention n'était destinée qu'à attirer l'attention.
Je ne souhaite pas faire autre chose et vous laisse le soin de continuer.
Si l'énoncé ne précise rien sur la direction de la vitesse initiale l'exercice est infaisable.
Peut être Othniel2 ne l'a t'il pas recopié fidèlement ?
***Edit gbm : si tu souhaites poursuivre avec eux, c'est avec plaisir, on lance le chantier de restructuration des fiches du forum, ça prend un temps fou  !***
!***
Je suis d'accord avec odbugt1, sans la direction de la vitesse initiale l'exercice est infaisable.
Il n'y a pas marqué que le tir effectué par l'enfant (l'élève?) est vertical ?
L'énoncé est tel , on néglige la résistance de l'air ..
Comme l'a précisé @odbugt1 il manque forcément l'angle avec lequel est lancé la balle.
Essaie de voir s'il n'y a pas une erreur d'énoncé du professeur, mais là je pense qu'il manque une donnée.
OK odbugt1 et si on utilisait
la variation de l'énergie cinétique qui est égale à la somme des travaux des forces extérieures en considérant que la vitesse finale est nulle au moment où l'objet redescend ?
OK odbugt1 et si on utilisait
la variation de l'énergie cinétique qui est égale à la somme des travaux des forces extérieures en considérant que la vitesse finale est nulle au moment où l'objet redescend ?
On a pas la masse de la balle...
Attention tout de même !
Sauf si le tir est vertical, personne n'a jamais vu un projectile s'arrêter au sommet de sa trajectoire !
Il est donc faux dans le cas général de dire que la vitesse de la boule est nulle au moment ou elle commence à redescendre.
Dans ce cas aidez moi à construire l'exo de sorte qu'il puisse être faisable .
Comment ça, tu construis tes propres exos ?
Il faut juste que tu donnes un angle de lancer, et avec la seconde loi de Newton trouver la flèche de la trajectoire.
OK et si je donnais 40° ?
avec la seconde loi de Newton trouver la flèche de la trajectoire. comment ?
OK et si je donnais 40° ?
avec la seconde loi de Newton trouver la flèche de la trajectoire. comment ?
En trouvant les équations horaires.
Il y a une fiche pour ça : Mouvement d'un projectile comme l'a précisé gbm.
Il faut chercher un peu par tes propres moyens, elle est dans la section terminale des fiches du forum : ![]() Mouvement d'un projectile dans le champ de pesanteur
Mouvement d'un projectile dans le champ de pesanteur

Le résultat dépend de l'angle du lancé avec le sol. Ta formule correspond à un lancé vertical( =90°). De manière plus générale, comme dit la fiche du forum, hmax=(V02sin2
=90°). De manière plus générale, comme dit la fiche du forum, hmax=(V02sin2 /2g)+h0
/2g)+h0
Bonjour , voici ce que j'ai trouvé :
Hmax=(Vo²/2g)+h
Avec
H max : la hauteur maximale .
Vo : la valeur de 4m/s
g: la pesanteur
h : la hauteur h=1,8m
AN:
Vo=4m/s ==>Vo²=16m²/s²
h=1,8m
g=10N/kg
==>Hmax=
Hmax=2,6m
Bonjour,
Non, ça dépend de l'angle que fait la vitesse initiale avec l'horizontale, comme la déjà dit iseioz le 3 janvier
Ok je sais que l'énoncé contient une erreur , à ce niveau-là et si on considérait que l'angle du lancé  =0° ou
=0° ou  =30° ? Puisqu'il s'agit d'un lancé non vertical du coup
=30° ? Puisqu'il s'agit d'un lancé non vertical du coup  ne peut pas atteindre 90° donc
ne peut pas atteindre 90° donc 
 [0°;90[
[0°;90[
Aidez moi à calculer la hauteur si  =30° par exemple .
=30° par exemple .
C'est expliqué en détail ici (calcul de la flèche)
![]() Mouvement d'un projectile dans le champ de pesanteur
Mouvement d'un projectile dans le champ de pesanteur
hmax= h + Vo2sin2 /(2g)
/(2g)
C'est la même situation physique: une chute libre avec vitesse initiale.
La seule difference est la condition initiale: z(0) = h (dans ton cas)
au lieu de z(0)=0 dans la fiche
Donc dans ton cas: K4 = h (et non pas 0) dans le calcul de z(t)
Ca ne change pas le principe du calcul.
seule la valeur finale de la flèche est impactée: h + Vo2sin2/(2g)
au lieu de Vo2sin2/(2g) dans la fiche
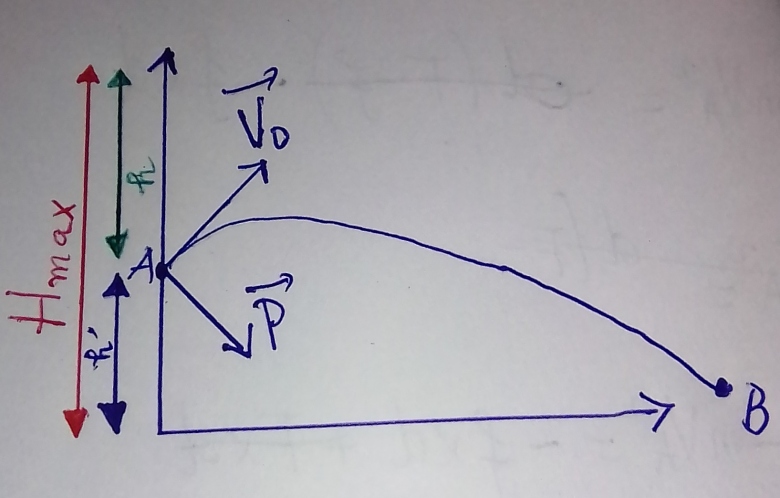
Peut être que vous n'avez pas bien compris l'énoncé...mais l'énoncé voudrait qu'on détermine la hauteur en rouge Hmax sur mon schéma ci-dessous .
Système : la boule
Référentiel : référentiel terrestre supposé galliéen.
Bilan des forces : le poids et la vitesse o.
Représentation : (voir schéma)
Appliquons le théorème de l'énergie cinétique.
∆ECA-B= WA-B
WA-Bext
==> ECB-ECA[/sub]=WA-B
Or ECB=0J
Donc 0-ECA=mgh
On retire
Si on simplifie m , on obtient :
==>
AN:VA²=16m²/s² ; g=10N/kg
|
|
Or Hmax=h'+h
Donc Hmax=0,8+1,8=2,6m
(et revoilà mes 2,6m). 
Peut être que tu devrais lire les réponses qu'on te fait...
Or EcB=0J
Donc 0-EcA=mgh
non ! ( je suppose que B est le sommet)
La vitesse au sommet N'EST PAS NULLE car la chute n'est pas verticale !
(remarque déjà faite pas odbugt1 l'an passé)
Bonjour à vous deux,
Je suis particulièrement ennuyé par la droite d'action et le sens du poids sur le schéma
 ...
...
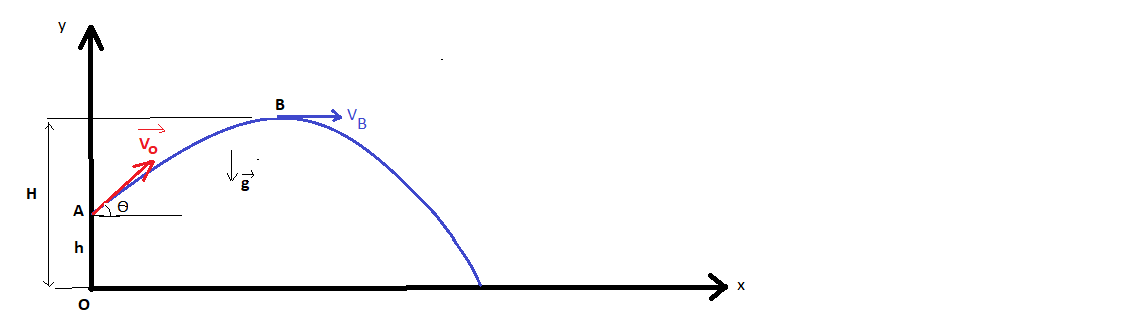
J'ai refait le dessin pour être plus précis.
La chute ne se fait pas uniquement selon la verticale (Oy)
La boule progresse aussi selon (Ox)
Et au sommet en B la vitesse de la boule n'est pas nulle (elle continue à avancer selon Ox)
Et le poids est dirigée selon (Oy), vers le bas !
Enfin, H = h + Vo2sin2 /(2g)
/(2g)
et si on vient en énergie cinétique , quelle formule utiliser ?
Tu peux appliquer à la boule, entre A et B :
- le théorème de l'énergie cinétique
- la conservation de l'énergie mécanique (si on neglige les frottements)
Ca te donnera la même équation, en fait.
on connait VA = Vo
mais il faudra calculer VB
en fait, c'est très simple, car le mouvement selon l'horizontale (Ox) est uniforme dans le cas d'une chute libre
(Vx reste constant) .
donc VB = Vo cos

Je te laisse le démontrer.
Bonjour à vous deux,
Je suis particulièrement ennuyé par la droite d'action et le sens du poids
 ...
...Gbm parlait de ton schéma , pas du mien .
Quant au théorème que tu cherches , c'est le théorème de l'énergie cinétique
Le système : la boule
Référentiel : référentiel terrestre supposé galliléen
Bilan des forces : le poids seulement ?