Bonsoir
Un signal périodique alternatif est un signal de valeur moyenne nulle. Le coefficient a_o de l'analyse de Fourier est donc nul. Supposons que ce signal ne possède que des harmoniques impaires. Ajoutons à ce signal une composante continue . Le signal n'est plus alternatif et pourtant, de son analyse de Fourier, seule la composante ao à changé. Ce signal, bien que non alternatif, ne possède donc que des harmoniques impaires.
Pour démontrer qu'un signal ne possède que des harmoniques impaires, il faut reprendre les expressions des différents coefficients comme cela est fait sur ton document.

D'accord merci
Mais quel signal ne possède que des harmoniques paires?, je ne trouve pas

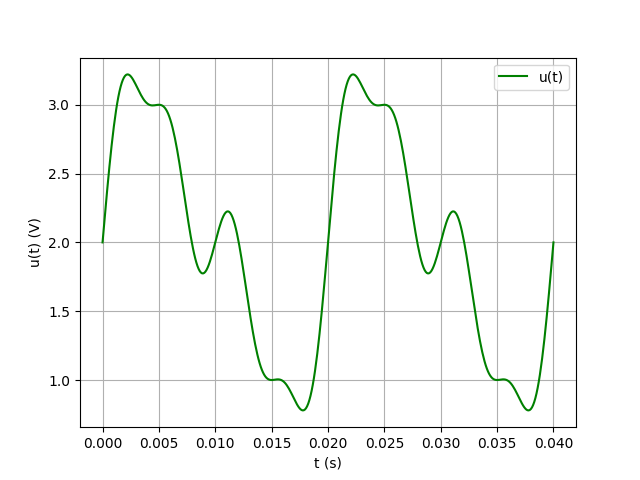
les signaux d'harmoniques uniquement pares se retrouvent en acoustique. Voici, à titre d'exemple, la représentation graphique sur deux période de :
u(t)=2+sin(w.t)+0.5.sin(2w.t)+0.25.sin(4w.t)

Merci,
Donc la raison (que j'ai donné au début) n'est pas bonne?

Je t'ai répondu hier soir à 23h49.

Ah désolé...

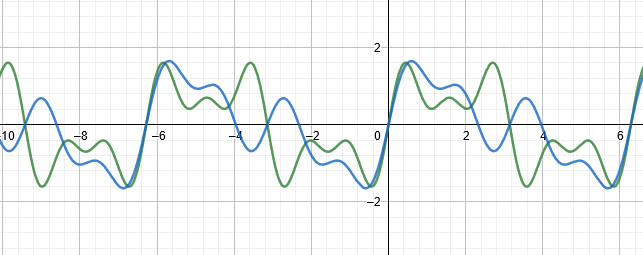
J'ai tracé deux expressions avec harmoniques paires (bleu) et harmoniques impaires (vert). Pour le signal avec des harmoniques paires, il n'y a pas de "symétrie" sur une période.

Donc vous me dites qu'à l'avance on ne peut pas savoir, il faut soit utiliser un oscilo ou calculer à la main

Je ne sais pas  ce que tu appelles "symétrie sur une période. Tes deux signaux ont au moins trois points communs :
1° fonctions impaires de t : série de sinus dans les deux cas.
2° signaux alternatifs dans les deux cas.
3° dans les deux cas, le point de l'axe horizontal de coordonnée (T/2) est centre de symétrie de la courbe sur une période :
entre zéro et T : quel que soit inférieur à T/2 :
u(T/2 + ) = -u(T/2-) .
On remarque aussi cette symétrie sur la partie alternative (u_AC=u - u_DC) de l'exemple que j'ai choisi dans mon précédent message.

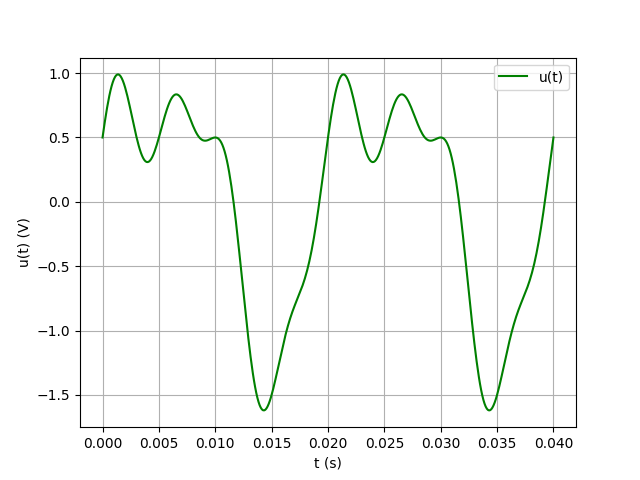
La symétrie évoquée au paragraphe 3 de mon précédent message disparaît si le signal fait apparaître à la fois des sinus et des cosinus.Voici par exemple, toujours sur deux périodes, la représentation graphique de :
u(t)=sin(w.t)+0,5.cos(2w.t)+0,25.sin(4w.t)
Le signal reste néanmoins périodique alternatif. En revanche, je ne vois pas trop à quel phénomène physique il peut correspondre...

D'accord merci beaucoup