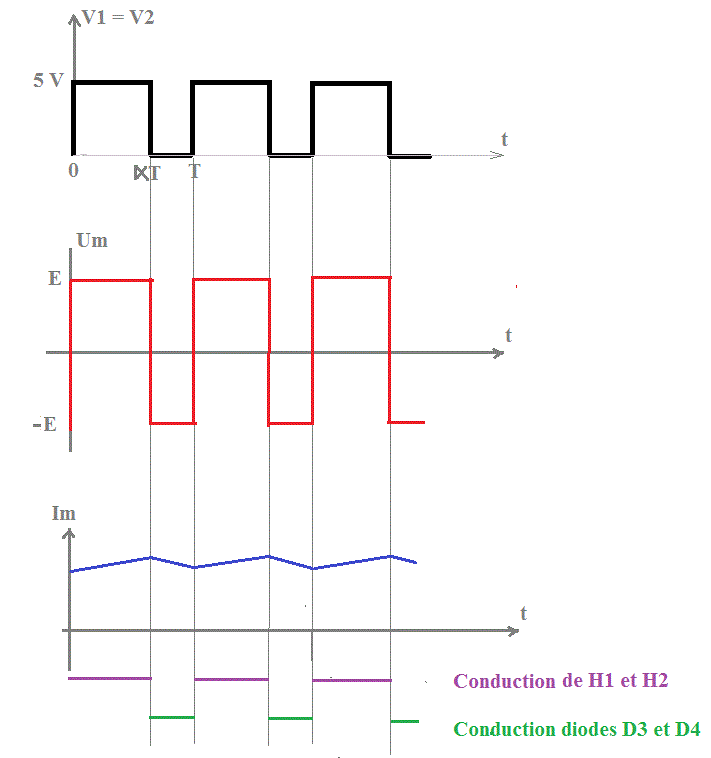
Um moyen = (E * (alpha * T) - E * (1 - alpha) * T)/T  (avec 0 <= alpha <= 1)

Um moyen = E * (2*alpha - 1)

Sauf distraction.  

Merci beaucoup !

Mais quelque chose me chiffonne, quand il y a une tension de 5V pour V1 et V2, c'est que les interrupteurs associés sont ouverts, non ? Dans ce cas comment H1 et H2 peuvent conduire ?

V1 et V2 sont les tensions gate-source des transistors correspondants.

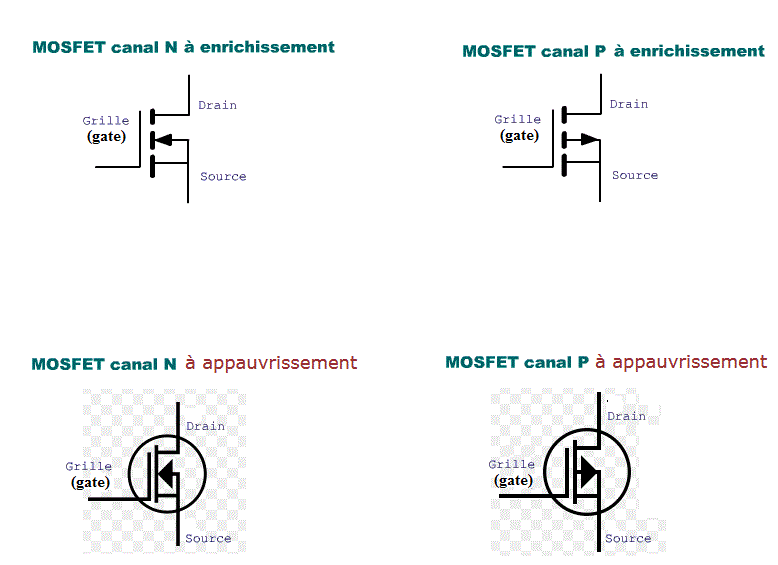
Les Transistors Mos représentés sur le schéma sont "N-Channel Enhancement Mode". (Canal N à enrichissement)

Comme par exemple celui  sur ce lien :

Ce type de transistor est conducteur avec une tension positive sur le gate par rapport à la source.

Il existe bien entendu aussi d'autres types de transistors Mos, par exemple le "Canal N à appauvrissement", ceux là conduisent au maximum si il y a 0 V entre le gate et la source, pour les bloquer, on doit appliquer une tension négative sur le gate par rapport à la source.

Et puis bien entendu, il existe les "P-Channel" à enrichissement et aussi à appauvrissement, dont le fonctionnement est similaire à leur "cousins" en N channel, mais évidemment en inversant toutes les tensions.



Sauf distraction.  

D'accord, je comprends mieux !

Merci en tout cas, ça m'a permis de bien avancé.

J'aurais une dernière question, dans le cas ou l'on ne néglige plus la résistance de l'induit, quelle serait l'allure du courant moteur ?

J'ai eu cette question en khôlle et je dois avoué que j'ai pas très bien compris les explications du khôlleur !

Il n'est nulle part écrit que la résistance d'induit était négligée dans ce qui a été fait.

C'est grâce à l'inductance d'induit que le courant ne change pas de sens (comme imposé par l'énoncé)

Et la tension calculée Um est celle aux bornes du moteur (donc inclut la force contre électromotrice et la tension aux bornes du bobinage d'induit (résistance et inductance incluses)

En fait si, dans les premières questions de mon sujet c'est marqué qu'il faut négliger la résistance.

Il faut d'abord tracer im en négligeant la résistance, et ensuite dans le cas où on ne la néglige pas.

J'ai réussi à répondre aux question calculatoires mais je bloque sur le tracé des courants.

On ne peut pas aller plus loin sans connaître les caractéristiques du moteur, la tension d'alimentation du hacheur, la fréquence du signal de commande ...

Mais de toutes manières, la tension Um a la forme que j'ai donnée. Il faut évidemment mettre une échelle sur chacun des axes à l'aide des données "tension d'alimentation du hacheur" et "fréquence du signal de commande".

Si on néglige R, alors E = Um(moyen)

Si on ne néglige pas R, alors E = Um(moyen) - R.Im(moyen)

Ceci, à la condition que la fréquence du hacheur soit bien supérieure à l'inverse des constantes de temps électrique et mécanique du moteur.

Avec toutes les données non communiquées ici connues, on pourra en plus calculer l'ondulation du Im.

Sauf distraction.  

Je ne l'ai pas mentionné, à tort :

Il faut aussi connaître les caractéristiques de la charge entraînée par le moteur (couple résistant) et si le problème à des "extensions dynamiques" (pour le démarrage, l'accélération ou le freinage) il faut aussi connaître le moment d'inertie de la charge (et celle du moteur) et ...

C'est de ma faute, j'aurais dû vous communiquer toutes les données:

Cr = 0,2 N.m

--> Im = 0,2/0,026 = 7,7 A

UN = 12 V = E' + R.I (en moyen)

E' = 12 - 0,6 * 7,7 = 7,38 V

w = E'/Km = 7,38/0,026 = 284 rad/s (2710 tr/min)
-----

Il manque encore comme donnée, la tension E du générateur.

Supposons qu'elle vaut 24 V, dans ce cas :

Um moyen = E * (2*alpha - 1)
12 = 24 * (2.alpha - 1)
alpha = 0,75

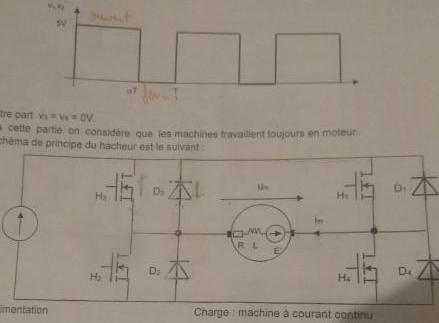
Comme T = 1 ms (visible sur document du début)

Le signal sur V1 et V2 est à + 5 volt pendant 0,75 * 1 = 0,75 ms et est à 0 V pendant 0,25 ms ... et puis cela recommence.

Cela n'est pas idéal comme hacheur car on n'a pas T < < L/R et donc, il y aura un fort taux d'ondulation du courant dans le moteur.

Amplitude crête à crête de l'ondulation courant : Delta I = (24 - 12 - 0,6 * 7,7)/L * alpha * T = (24 - 12 - 0,6 * 7,7)/10^-3 * 0,75 * 10^-3 = 5,54 A

Im ondule donc entre (7,7 - 5,54/2) = 4,9 A et (7,7 + 5,54/2) = 10,3 A

Ca, c'est un calcul approché, on peut peaufiner en établissant l'équation différentielle ad-hoc ...
-----
Dans le cas où on aurait R = 0, alors on aurait E' = 12 V (FCEM moteur)
--> w = 12/0,026 = 461 rad/s (4402 tr/min)

et Delta I = 12/L * alpha T = 9 A

Im ondulerait donc entre (7,7 - 9/2) = 3,2 A et (7,7 + 9/2) = 12,2 A
-----
Aucun calcul vérifié.

Merci pour ces détails!

Le générateur (Vbat) délivre une tension de 12 V, ce qui voudrait dire que Alpha est égale à un, alors que ce n'est pas possible, non ?

Si le générateur délivre 12 V, alors pour avoir Um = 12 V, il ne peut pas y avoir de hachage.

Pour avoir du hachage, il faut absolument que U générateur > Um

Il faut recopier l'énoncé intégralement.

Et attention, sur ce site, on ne peut pas envoyer de scan d'énoncé, il faut obligatoirement écrire soi-même l'énoncé.
Seuls les dessins sont autorisés comme image.

Eh bien par exemple dans une question on me demande de démontrer que l'ondulation peut se mettre sous la forme: 2[(1-alpha)alpha/Lf] Vbat

J'ai réussie à le démontrer, mais par la suite on me demande dans un premier temps de déterminer la valeur de alpha pour laquelle l'ondulation est maximal.

Ensuite, pour Vbat=12v et T=50μs, on me demande de déterminer numériquement la valeur de l'ondulation maximale.

Dans une autre question on me demande de justifier que la vitesse de rotation du moteur s'obtient par W=a*aplha+b.
Il faut identifier a et b.

Ce sont les deux seules questions qui me bloquent je pense.

De plus, vous pouvez voir sur le schéma que Vbat est bien égal à 12v....

Voici le schéma en question

Mince, excusez moi j'avais oublié d'attacher l'image...

Bonsoir à vous deux,

@sgotsk : attention à bien respecter la règle qui suit

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Voici l'énoncé précis:

Deux moteurs participent simultanément à l'action sur le hayon. Chacun est géré par un module de commande doté d'une interface de communication :
CAN et LIN pour le moteur Maître, LIN pour le moteur Esclave.
L'objectif de cette partie est de valider la solution retenue pour la motorisation de
l'ouvrant, dans le cadre d'une commande d'ouverture.
III.D.1) Chaque moteur est géré par un module de commande associé à un
hacheur quatre quadrants :


On considérera comme idéaux les transistors MOSFET:

Si VGS>4v alors Vk=0v; Etat passant
Si VGS=0 alors iDs=0A; Etat bloqué

On considérera comme idéale la diode: tension seuil Vd=0v lorsqu'elle est passante.

Le MCC à aimants permanents est assimilé à une charge (Rm, Lm, E)



Le moteur est associé à un réducteur de rapport de réduction de que l'on
considérera sans perte. On considère le cas correspondant à un point de fonctionnement
en régime établi : la vitesse de rotation est constante et le couple
mécanique demandé à chaque moteur est . La commande est telle que le courant ne s'annule pas (régime de conduction continue présentant
une ondulation autour d'une valeur moyenne).
Les signaux de commande et sont
identiques, de période : signal
logique de rapport cyclique compris entre
0.5 et 1 . D'autre part V3 =V4=0 .
Dans cette partie on considère que les
machines travaillent toujours en moteur.

d) Justifier que la vitesse de rotation du moteur s'obtient par la relation : Ω = a ⋅ α + b. Identifier les expressions de a et b.
Calculer la valeur de  aplha pour obtenir le point de fonctionnement défini par
Ω 115 rd s-1 avec  Cr = 0 2 N m , ⋅ Vbat = 12 V avec et .
e) Proposer une stratégie de commande à la fermeture des interrupteurs permettant
d'assurer la fermeture du coffre en sachant que les machines travaillent
en moteur.

Merci beaucoup, tout est clair maintenant (enfin j'espère ^^)