Bonsoir,

Oui ils sont complementaires.
mais thyristor en // avec une diodepas un triac non.
Merci

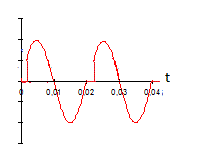
Courant et tension ont la même "allure" puisque la charge est résistive.



Les "échelles" des graphes sont faciles à trouver.

Sauf distraction.  

Merci pour le schema je vois bien pendant alternance (-V) nous avont toute la sinusoide cela correspond-il au moment où la diode conduit?
et pour le calcul de
or mon angle d'amorçage du thyristor est de 30° si je fais l'application numerique avec valeur de je trouve ce qui est sous la racine negative c'est où mon erreur?
Merci d'avance

Et sauf erreur, cela donne:
  


Et Bien entendu: Ieff = Ueff/R

Vm est la tension crète de la sinusoïde et donc ici : Vm = 500*V2 = 707 V

Avec alpha = 30° (Pi/6), on trouve Ueff = 404 V.

Avec alpha = 180° (Pi), on trouve

Vérifie.

Oui moi javais integré sur [,2]. ce qui est faux je suppose
Mais je trouve encore
j'ai du faire une erreur quelque part

Ouiii c tout bon pour la verification c'est moi en voulant simplifier vite les choses.
Merci des reponses ça me permet d'avancer
Et le faite integrer [,2] ne va pas?

bonsoir
on intègre de façon que la période du signal soit de [2]pi.
dc on intègre de [alpha,[2]pi +alpha].
on fait un changement  de variable pour pouvoir utliser les angles, on pose par exemple theta=omega*t=[2]pi*f*t

Attention.

Il faut savoir ce qu'est l'angle alpha.

En général, on désigne par alpha l'angle de conduction du thytistor.
Alpha = 0  signifie que le thyristor n'est jamais passant.
Alpha = Pi signifie que le thyristor est passant en permanence sur l'alternance qui le permet évidemment.

La tension sur la charge que j'ai écrite l'est sous cette définition de alpha.
-----

Si on désigne par alpha, l'angle pendant lequel le thyristor n'est pas enclenché ou ce qui revient au même l'angle que l'on attend (par rapport au début de l'alternance où le thyristor peut être enclenché) avant d'envoyer l'impulsion de gate sur le thyristor alors il faut en tenir compte en changeant les bornes d'intégration.
-----

biensur qu'il faut en tenir compte pour celui qui veut utiliser des bornes temporelles pour l'integration.
sinon ça fait    [ α,2π+α] pour celui qui veut utiliser les angles

Bonsoir,
precision
est l'angle de retard à amoçage du thyristor.

tibila,

Tu n'as pas compris mon message.

Ce que j'ai écrit reste valable que l'on considère les angles ou les temps.



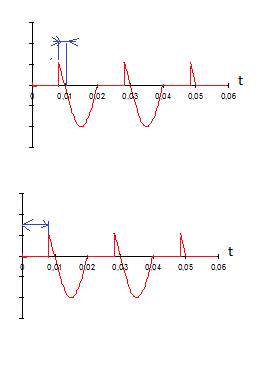
Habituellement, on appelle alpha l'angle de conduction du thyristor qui correspond à la durée de conduction repérée en bleu sur le dessin du haut.

A ne pas confondre avec l'angle auquel on allume le thyristor, qui correspond à la durée bleue sur mon dessin du bas.
-----
Il est évident que suivant la "définition" utilisée pour alpha, il faut en tenir compte dans les bornes d'intégration.

Moi, j'ai utilisé ce qui se fait le plus souvent, soit la définition de alpha correpondant à la durée de conduction du thyristor comme sur le dessin du haut.
-----
De toutes manières, il ne faut pas intégrer le carré de la sinusoïde sur toute une période comme tu le proposes, sinon tu trouveras systématiquement Vmax/V2 comme valeur de Ueff.

Si on comprend alpha comme je l'ai fait, on doit intégrer  V[(1/(2Pi)).V²m.sin²...] depuis Pi-alpha jusque 2Pi

Si on comprend alpha comme sur le dessin du bas, on doit intégrer  V[(1/(2Pi)).V²m.sin²...] depuis alpha jusque 2Pi.

filleule

Si alpha est l'angle d'amorçage du thyristor, alors c'est comme sur le dessin du bas.
C'est bien triste car contraire aux "habitudes", mais soit.

Il suffit de remarquer que le alpha de ma formule doit être remplacé par Pi - alpha pour avoir la relation qui correspond à ton cas.

On arrive alors à :

Sauf distraction.  

donc maintenant j'ai

on va pas jusqu'a 2 comme elle est nulle à cette partie on s'arrete à juste 2
Si Ok les bornes integration,
je trouve
confirmation

la tension etant  nulle sur [2π,2π+α[  on peut  s'arreter à 2π,
ce qui revient à integrer sur [α,2π].d'où l'ulisation de l'intervalle [α,2π] justitiée!!!

je trouve la meme expression.

En appelant alpha l'angle d'amorçage, alors pour alpha = 30° le dessin devient ceci :

C'est compris merci pour votre aide.