Niveau licence

Gouttes d'eau (thermodynamique)

Posté par
Pikimidb 02-01-18 à 18:39

Bonsoir,

Je fais un exercice assez long, et je bloque à un (voir plusieurs) endroit, voici l'énoncé et mes réponses  :

On considère un système à T, p fixés par un réservoir de pression et de température. Dans ce système, on place deux petites gouttes d'eau sphériques chacune de volume V0. On considère que le gaz est en équilibre avec les deux gouttes et on ne considèrera que les deux gouttes liquides pour la suite, en admettant que le gaz se comporte comme une
membrane perméable à l'eau. Si la goutte est suffisament petite, on peut montrer que la pression à l'intérieur d'une goutte est donnée par la relation :
p = p0 +2/R
où R est le rayon de la goutte. est la tension de surface eau/air et est considérée comme une constante. On admettra ce résultat. On rappelle que le volume V d'une sphère de rayon R vaut :
V = 4/3 * R³

1. Si on note vN le volume par particule dans la phase liquide, que vaut vN en fonction de R0 et de N0 le nombre de particules dans la goutte ?

vN = V/N0 = $\frac{4/3\pi R0^3}{N0}$

2. On rappelle que :   = 0 + vN (p − p0) où vN est le volume par particules et p la pression du liquide et µ0 le
potentiel chimique standard à p0. Que vaut l'enthalpie libre Gg pour une goutte en fonction de R0, N0, p0, , vN et 0 (On utilisera la relation de Gibbs-Duhem G = N). En déduire l'enthalpie libre totale initiale G0 des deux gouttes.

J'ai trouvé que Gg = NO0+8/3 * R0₂
Et que G0 = 2.Gg.

3. Les deux gouttes ont la même taille. Elles ont la même température. Que peut-on dire de la pression et du potentiel chimique de l'eau dans ces deux gouttes ? Le système est-il à l'équilibre ?

Ca je ne suis pas trop sûr, mais j'ai mis que la pression et le potentiel chimique de l'eau sont les mêmes dans les deux gouttes (sans trop savoir pourquoi...). Le système serait donc  à l'équilibre.

4. Les deux gouttes peuvent échanger des particules par l'intermédiaire de la phase gaz. On suppose qu'une goutte (qu'on appelle 1) a perdu N molécules et que l'autre goutte (2) a gagné N molécules. En utilisant la conservation de la quantité de matière, montrer que :
$\frac{R1}{R0} = (1-\frac{N}{N0})^\frac{1}{3}\ et\ que\ \frac{R2}{R0} = (1+\frac{N}{N0})^\frac{1}{3}$

Ca c'est bon.

5. On peut calculer une nouvelle enthalpie libre G contrainte par ce nombre de particules. Exprimer G1 l'entalpie libre de la goutte 1 en fonction de son rayon R1 et de G2 en fonction de son rayon R2.

J'ai trouvé G1  = (R1/R0)³(N00+8/3 * R1²)
Et G2  = (R2/R0)³(N00+8/3 * R2²).

6. En notant x = N/N0, en déduire que l'enthalpie libre totale du système à deux gouttes s'écrit :
$GN = G0 + \frac{2 \gamma v_N N_0}{R_0}((1-x)^\frac{2}{3} + (1+x)^\frac{2}{3} - 2)$

Ca je n'ai pas réussi.

7. Que vaut GN − G0 quand x = 0 et x = 1 ? Que peut-on en déduire sur l'évolution spontanée des deux gouttes initiallement de même taille ? Est-ce un système à l'équilibre ?

On trouve 0 dans les deux cas, donc je suppose que le système a deux équilibres mais je ne sais pas trop là non plus.

8. Que vaut ∂GN /∂x en x = 0. Pourquoi peut-on attendre ce résultat ?

J'ai trouvé une valeur de :
G0 - $\frac{4\gamma V_NN0}{R0}$
Mais je ne sais pas quoi en dire.

Le reste je ne l'ai pas encore fait.
9. On veut montrer que le système est initialement instable. Pour ce faire, on va montrer qu'une petite fluctuation
de taille autour de R0 va être amplifiée. Calculer la dérivée seconde de GN : ∂
2GN /∂x2 pour x ∼ 0. En déduire la forme de la courbe GN (x) au voisinage de x ∼ 0. Pourquoi la fluctuation de taille va être amplifiée ?

10. Que se passerait-il si on avait préparé dès le départ deux gouttes de tailles différentes ?

11. Jusqu'à présent, nous avons considéré une goutte d'eau pure. Nous rajoutons maintenant une faible fraction de sel dans les gouttes, le sel ne pouvant pas être échangé entre les gouttes. Comment l'équilibre final va-t-il être modifié ?

Posté par re : Gouttes d'eau (thermodynamique) 03-01-18 à 20:59

Posté par re : Gouttes d'eau (thermodynamique) 04-01-18 à 15:03

Bonjour
Tout ce que tu as fait jusqu'à la question 5 me semble correct sauf un oubli d'un “ $\gamma$ ” en 2). Je préfère écrire les expressions des enthalpies libres des deux gouttes ainsi :

$G_{1}=\left(N_{0}-N\right)\mu^{0}+\frac{8\pi\gamma}{3}R_{1}^{2}\quad;\quad G_{2}=\left(N_{0}+N\right)\mu^{0}+\frac{8\pi\gamma}{3}R_{2}^{2}$

$G_{N}=G_{1}+G_{2}=2N_{0}\mu^{0}+\frac{8\pi\gamma}{3}R_{0}^{2}\left[\left(1-x\right)^{\frac{2}{3}}+\left(1+x\right)^{\frac{2}{3}}\right]$
Selon le résultat de la question 2) :

$G_{0}=2\left[N_{0}\mu^{0}+\frac{8\pi\gamma}{3}R_{0}^{2}\right]$
Donc :

$G_{N}=G_{0}+\frac{8\pi\gamma}{3}R_{0}^{2}\left[\left(1-x\right)^{\frac{2}{3}}+\left(1+x\right)^{\frac{2}{3}}-2\right]=G_{0}+\frac{2\gamma.v_{N}.N_{0}}{R_{0}}\left[\left(1-x\right)^{\frac{2}{3}}+\left(1+x\right)^{\frac{2}{3}}-2\right]$
Pour 7 : la situation x=0 correspond aux deux gouttes identiques. Il est donc logique d'obtenir : $G_{N}=G_{0}$ . Attention : ce n'est pas le cas en x = 1 (revois ton calcul) ; cette situation limite correspondrait à une seule goutte contenant toutes les molécules d'eau.

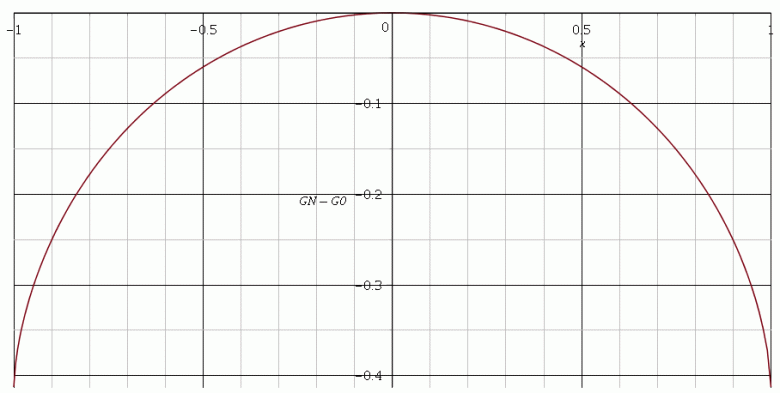
Pour comprendre la suite, il faut avoir en tête les propriétés de l'enthalpie libre d'un système fermé susceptible d'évoluer à température et à pression constante. Une évolution spontanée du système n'est possible que si G diminue au cours de l'évolution. Toute augmentation de G étant impossible, un état d'équilibre stable correspond nécessairement à un minimum de G. Je te fournis la courbe correspondant aux variations de $G_{N}-G_{0}$ en fonction de x (échelle des ordonnées totalement arbitraire). Le cas limite x=-1 correspond à toutes les molécules rassemblées dans la goutte n° 1 et le cas x = 1 correspond à toutes les molécules rassemblées dans la goutte n° 2. On voit clairement qu'il n'existe pas d'état l'équilibre en présence des deux gouttes : les molécules d'eau vont tendre à se regrouper en une seule goutte... mais j'anticipe...

$Gouttes d\'eau (thermodynamique)$

Posté par re : Gouttes d'eau (thermodynamique) 05-01-18 à 15:42

Bonjour

Merci beaucoup pour l'aide et la courbe !

J'ai refait le calcul pour x = 1, j'ai trouvé quelque chose de négatif, j'ai donc écrit :

G_N - G₀ < 0 => G_N(1)<G_N(0), le système va évoluer afin d'atteindre cet état de plus basse enthalpie libre pour une évolution spontanée (soit 1 seul goutte).
Le système est donc dans un équilibre instable.

8) J'ai trouvé 0 pour x = 0, ce résultat est logique puisque pour x = 0, le système est à l'équilibre (donc la pente de la courbe est nulle).

9) J'ai fait le développement limité à l'ordre 2 de G_N (je ne sais pas si c'est ce qui est attendu) :
$G_N \sim G_0 + \frac{2\gamma V_N N_0}{R_0}(1-\frac{2}{3}x-\frac{1}{9}x^2 + 1 + \frac{2}{3}x - \frac{1}{9}x^2 -2) = G_0 + \frac{2\gamma V_N N_0}{R_0}(-\frac{2}{9}x^2)$ .

La forme de la courbe est donc une parabole "négative".
Ainsi, pour une petite perturbation autour de la position d'équilibre, la perturbation va être amplifiée (j'ai fait un schéma de la courbe pour expliquer).

10) Pour 2 gouttes de tailles différentes, l'enthalpie libre de la goutte la plus grosse serait grande, toutes les molécules se réuniraient vers la goutte la plus petite ? (je ne suis pas sûr ici).

11) Ici je ne sais pas trop, je pense que c'est en rapport avec le potentiel chimique, mais je n'arrive pas trop à visualiser ce qu'il se passerait, l'équilibre ne serait pas aléatoirement déplacé vers une goutte ou l'autre ?

Posté par re : Gouttes d'eau (thermodynamique) 05-01-18 à 16:00

Tu sembles avoir très bien compris. Erreur tout de même à la question 10.
Suppose x>0 : N1<N2 ; la goutte la plus grosse est la n° 2 , l'évolution spontanée va se faire de sorte que x augmente jusqu'à 1 donc jusqu'à la disparition de la goutte n° 1.
Suppose x<1 : N1>N2 : la goutte la plus grosse est la n° 1. L'évolution spontanée va se faire de sorte que x diminue jusqu'à (-1) donc jusqu'à la diminution de la goutte n° 2.
L'évolution spontanée correspond donc à un transfert de matière de la plus petite vers la plus grosse des deux gouttes jusqu'à un état final constitué d'une seule goutte.

Posté par re : Gouttes d'eau (thermodynamique) 05-01-18 à 16:22

D'accord, je comprends mieux !
Est-ce que on peut l'expliquer avec la courbe également, en prenant différents point initiaux ? (un peu comme en mécanique pour l'énergie potentielle)

Pour la 11) je ne sais pas si il faut considérer qu'on met la même quantité de sel dans les 2 gouttes (et si elles ont la même taille).

Posté par re : Gouttes d'eau (thermodynamique) 05-01-18 à 17:29

Citation :
Est-ce que on peut l'expliquer avec la courbe également

Bien sûr ! C'est graphiquement que l'on montre le plus simplement que x tend vers 1 ou -1 selon le signe initial de x.
Concernant la dernière question, j'avoue ne pas comprendre exactement ce qu'attend le concepteur de l'énoncé. Il est question d'une très petite quantité de sel. On peut donc penser que le transfert d'eau s'effectue dans un premier temps comme prévue par la théorie précédente. Alors, la concentration en sel devient de plus en plus grande dans la goutte la plus petite et de plus en plus faible dans la goutte la plus grosse. Le potentiel chimique de l'eau varie : il diminue dans la goutte la plus petite et augmente dans la goutte la plus grosse. On peut alors imaginer un transfert de matière du potentiel chimique le plus élevé vers le potentiel chimique le plus faible analogue au phénomène d'osmose de sorte qu'un état d'équilibre soit atteint avant disparition intégrale de la goutte la plus petite.
Sous toutes réserves...

Posté par re : Gouttes d'eau (thermodynamique) 05-01-18 à 17:39

Ok !
Merci beaucoup !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Gouttes d'eau (thermodynamique)

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique