Bonjour
Et si tu fournissais un énoncé complet du problème accompagné si possible d un scan du schéma qui l'accompagne ? Tu ne précises pas l'axe de rotation. Le système est-il abandonné à lui-même dans le champ de pesanteur ? Peu probable vue la position initiale de la gomme... un moteur impose t il à la règle un mouvement de rotation précis  ( uniforme par exemple) ?

Dans un repère en rotation uniforme par rapport à un repère galiléen :
La force d'inertie de Coriolis ne travaille pas. On peut lui associer une énergie potentielle nulle.
En coordonnées polaires, l'énergie potentielle associée à la force d'inertie d'entraînement vaut :


Je te laisse faire la démonstration.

Désolé  : oubli du signe "-" dans l'expression de l'énergie potentielle associée à la force d'inertie d'entraînement centrifuge.

Bonjour vanoise et merci de ta réponse, voici l'image en pièce jointe

oupss j'ai oublié d'attacher

Quelle est la question posée??? Peut-être déterminer à partir de quelle valeur de la gomme quitte la tige ? Si oui, l'étude peut se mener en deux étapes.
1. Considérer la gomme immobile par rapport à la tige et, en raisonnant sur la conservation de l'énergie mécanique de l'ensemble (tige-gomme ), établir les expressions en fonction de   de la vitesse angulaire et de l'accélération angulaire.
2. Faire une étude statique de la gomme dans le repère tournant lié à la tige et, en appliquant les lois de Coulomb sur les frottements solides, répondre à la question.
Tout cela sous réserve bien sûr, sans énoncé complet...

Juste une précision : pour l'étape 2, je t'ai suggéré de travailler dans le repère tournant lié à la tige dans la mesure où tu as évoqué les forces d'inertie. C'est une bonne méthode mais il est aussi possible de continuer à raisonner dans le repère terrestre galiléen. L'essentiel en mécanique est de toujours bien préciser le système étudié et le repère d'étude.

Bonjour vanoise et merci de ta réponse;
voici l'énoncé :
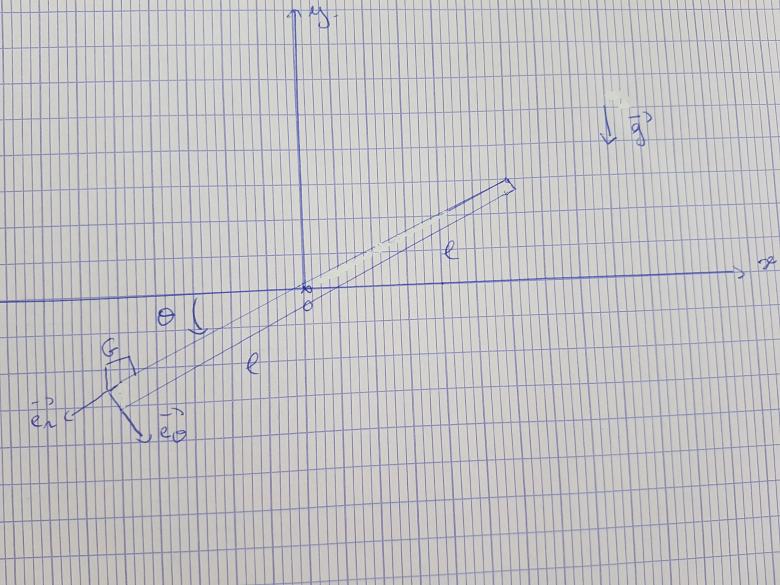
Une gomme assimilée à un point matériel G de masse m est posée au bout d'une règle ( longueur 2l, masse M, moment d'inertie (1/3)Ml². Au départ, la règle est immobile et horizontale puis elle tourne autour de l'axe Oz sans frottement. La règle fait, à t, l'angle
θ(t) avec sa position initiale. Le coefficient de frottement de la gomme est f0.
1) Par de considérations énergétiques, donner une relation entre θ et dθ/dt ( comme tu l'as dit vanoise : conservation de l'énergie mécanique)
2) Dans la base (er, eθ) , donner en fonction de θ la réaction exercée par la règle sur la gomme. ( ????)
3) Déterminer l'angle θi à partir duquel la gomme tombe de la règle. (????)

Mercii de ton temps.

C'est donc exactement ce que j'avais imaginé !
Qu'as-tu obtenu en 1) ?
Pour la 2 : vue la suite du problème, inutile de changer de repère. Il suffit d'appliquer la RFD à la gomme animée par rapport à la terre d'un mouvement circulaire non uniforme, en notant N la réaction normale de la règle sur la gomme et T la réaction tangentielle de la règle sur la gomme. Connais-tu les lois de Coulomb sur les frottements solides ?

Bonsoir vanoise,
par application de la conservation de l'énergie mécanique j'ai trouvé:
Jéq*d²θ/d²t +mgrcos(θ )=0
où je note Jéq le moment d'inertie équivalent de la gomme plus la règle autour de (oz) et r= ||OG||  qui caractérise la position de la gomme …. j'ai pris r constante
J'ai résonné ainsi:
énergie mécanique = énergie cinétique gomme(mouvement de rotation autour d'un axe fixe donc = moment d'inertie*(vitesse de rotation)²) + énergie potentielle de pesanteur de la gomme + énergie cinétique règle ( mouvement de rotation autour d'un axe fixe donc = moment d'inertie*(vitesse de rotation)²)
…..
Sinon, mon problème avec cet exo est que j'arrive pas à interpréter en termes physiques "glissement de la gomme" :... la réaction de la règle s'annule ??    

Le repère d'étude est le repère terrestre considéré comme galiléen. La gomme est assimilée à un point matériel de masse m posé à la distance l du centre de la règle. Le fait que la gomme soit à l'extrémité de la règle est fondamental pour bien comprendre la situation. Dès que la tige penche comme sur ton schéma, la gomme a tendance à glisser et à tomber de la règle mais, tant que la pente n'est pas trop forte, la composante tangentielle de la force exercée par la règle sur la gomme empêche cette chute. On peut donc, pour les questions 1 et 2, considérer la gomme immobile par rapport à la règle. On peut donc poser r=constante=l.
Question 1 : on considère l'ensemble {règle - gomme} comme un seul solide dont le moment d'inertie par rapport à l'axe de rotation est :


Ce solide est mobile autour d'un axe fixe. Son énergie cinétique est :



Les frottement étant négligés, la seule force susceptible de travailler est le poids de la masse m. En choisissant comme altitude de référence l'altitude du centre O, l'altitude de la gomme est . D'où l'énergie potentielle :


L'énergie mécanique initiale étant nulle avec ces conventions, la conservation de l'énergie mécanique conduit à :



soit :



En dérivant l'expression précédente par rapport à t puis en simplifiant par la vitesse angulaire non nulle au cours du mouvement, on obtient :



Pour la question 2 : il faut appliquer la RFD à la gomme seule en la supposant toujours immobile par rapport à la règle. Sa vitesse angulaire et son accélération angulaire sont celles qui viennent d'être calculées. On peut écrire l'expression de la force exercée par la règle sur la gomme sous la forme :

(voir mon message précédent)

Pour la question 3, il suffit d'écrire que la gomme reste sur la règle tant que :



Sinon, la règle tombe.
Je te laisse réfléchir à tout cela et continuer...

Merci vanoise ta réponse est très claire, j'ai très bien compris