Inscription / Connexion Nouveau Sujet
Géomètre des masses
Bonjour à tous. Désolé pour la saturation ces derniers temps mais j'ai vraiment envie de dissiper totalement mes lacunes en mécanique.
En effet pour un solide fixe dans un référentiel galiléen R(O,x,y,z) lorsqu'on me demande de déterminer soit les coordonnées du centre d'inertie de du solide, soit du moment d'inertie je le fais sans aucune difficulté. Pour déterminer la matrice d'inertie par rapport à G, je détermine dans un premier temps celle par rapport à O et je déduis par le théorème d'huygens généralisé.
Maintenant lorsque j'ai à faire à un solide mobile je n'arrive plus à faire. Je pense que dans ce cas les coordonnées de G dépendront du temps et je ne sais pas trop pour les deux autres.
On a défini toutes ces notions pour des solides fixes. Ces grandeurs se calculant par des intégrales, il m'est difficile de placer les bornes des bornes dans ce cas pour déterminer les différentes expressions.
Bonsoir
Le théorème de Huygens généralisé te donne une relation entre le tenseur d'inertie en un point A quelconque et le tenseur d'inertie en G que ces points soient fixes ou non. Si les points sont mobiles les tenseurs d'inerties sont définies à une date t et t intervient dans le résultat. Bien sûr, pour être plus précis, il faudrait un énoncé complet avec un schéma...
Ok monsieur. En parlant de précision, voici un petit exercice dans ce sens.
On considère un disque de masse m et de rayon R dont le centre varie suivant la loi xG= f(t) yG=g(t) et zG=h(t). Ce disque tourne autour de l'axe (Oz) avec une vitesse angulaire=j(t). On demande de déterminer le moment d'inertie par rapport à Gy. Ensuite on demande le moment cinétique en G.
Concernant la première question, IGy= l'intégrale de (x2+z2)dm. Mais placer les bornes me dépasse. Pour calculer le moment cinétique, je pense que je dois d'abord chercher la matrice d'inertie en G. Sur les bases de ce que vous avez dit, pour trouver cette matrice d'inertie en G, je vais d'abord la calculer en O mais là il y aura encore des intégrales à calculer.. Ayant réussi à le faire ( chose que je n'ai pas pu jusqu'ici), je remplace dans la formule ci bas les coordonnées de x dépendant du temps et je déduis.
Monsieur j'espère que j'ai bien explicité mon problème et j'aimerai surmonter cette difficulté. Merci.
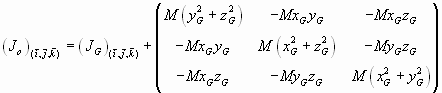
Il s'agit d'un disque donc d'un cylindre d'épaisseur négligeable. Si (Gz) désigne l'axe perpendiculaire au plan du disque, on peut poser z=0 pour toute masse élémentaire dm.
Ainsi :
Par raison de symétrie, ces deux moments d'inertie sont égaux ; ainsi :
Ce dernier moment d'inertie est facile à calculer en utilisant les coordonnées polaires. Tu remarqueras l'analogie de raisonnement avec les cas de la sphère et de la boule.
Donc monsieur si j'ai bien compris, pour déterminer la matrice en O on résoud comme pour un solide solide fixe. En d'autres termes la matrice en O ne dépendra par du temps et celle en G sera fonction du temps comme les coordonnées de G dépendent eux même du temps. C'est bien ça ?



