Bonjour,
Et si tu proposais un début de solution en expliquant éventuellement ce que tu ne comprends pas. Il sera plus facile de t'aider ensuite...
Qu'appelles-tu exactement rapport molaire B/A ?

Bonjour,
Merci pour la réponse. Le rapport molaire A/B=1/5 c'est le rapport entre les débits molaires des substances A et B qui entrent dans le réacteur.
j'ai déjà fait l'inventaire des nombres de variables et des nombres d'équations, en tenant compte des nombres de spécifications de compositions et de débits du système mais j'ai trouvé un degrés de liberté  du procédé non nul .J'ai essayé de trouver une base de calcul mais ça marche pas.

J'hésitais entre rapport molaire d'entrée ou de sortie du réacteur...
Voici un raisonnement possible qui a le mérite de permettre de calculer tous les débits molaires en fonction du débit molaire d'entrée mais il y a peut-être plus simple s'il s'agit juste d'obtenir le taux de conversion que je note r.
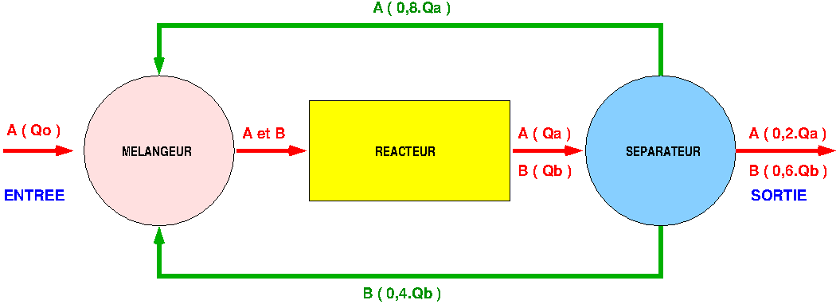
Je joins un schéma récapitulatif du fonctionnement avec entre parenthèses les divers débits molaires exprimés en fonction du débit molaire d'entrée Qo et des débits molaires de sortie du réacteur notés Qa et Qb.
Le fait que le débit d'entrée dans le réacteur est 5 fois plus important pour A que pour B conduit à l'équation :
Qo+0,8Qa=5*0,4Qb=2Qb
Le débit de sortie de B est égal au débit d'entrée de B augmenté de "r" fois le débit d'entrée de A :
Qb=0,4Qb + r(Qo + 0,8Qa)
En combinant les deux équations, on obtient :
Qb=0,4Qb + 2r.Qb
Puisque : Qb0 on obtient : r = 0,3 soit 30%
Il est alors possible d'exprimer les débits molaires Qa et Qb en fonction de Qo le débit d'entrée.

Bonjour,
Merci encore.
Mais moi je n'ai pas compris l'équation Qo+0,8Qa=5*0,4Qb=2Qb .
La somme des débits du substance A à l'entrée doit être égale à la somme des débits du substance A à la sortie .
Mais dans cette équation je vois pas cela .
Et comment traduisez-vous en terme de composition (% ou titre molaire) le rapport molaire 1/5=A/B ?

Tout est sur le schéma !
Le débit d'entrée de A dans le réacteur est la somme du débit Qo et du débit renvoyé à partir du séparateur : 0,8Qa
Le débit  d'entrée de B dans le réacteur est uniquement le débit renvoyé à partir du séparateur : 0,4Qb.
Si le débit d'entrée de A dans le réacteur est 5 fois supérieur au débit d'entrée de B dans le réacteur, cela donne bien l'équation que j'ai écrite.

Je ne comprend pas pourquoi le débit  d'entrée de B dans le réacteur est uniquement le débit renvoyé à partir du séparateur : 0,4Qb ? vu que les deux courants sont différents .

Bonjour,

Merci encore,
je comprend la première équation.
mais concernant la relation entre le taux r et Qb   " Qb=0,4Qb + r(Qo + 0,8Qa)  " vous pouvez m'expliquer pourquoi ?
par ce que  moi je connais une formule de r  :
                r=( (Qo + 0,8Qa )-Qa) / (Qo + 0,8Qa)  par exemple ici.

Ta méthode conduit au même résultat !
Tu définis r comme le rapport : (diminution du débit de A)/(débit d'entrée de A dans le réacteur). C'est une bonne définition !
Seulement, comme la réaction se produit mole à mole, la diminution du débit de A dans le réacteur est égale à l'augmentation du débit de B dans ce même réacteur.
r=(Qb-0,4Qb)/(Qo+0,8Qa)
Comme j'ai démontré avant : Qo+0,8Qa=2Qb, cela conduit bien à :
r=0,6Qb/(2Qb)=0,3 (30%)

Bonjour,
Merci pour votre aide j'ai bien compris maintenant.
         Merci