Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Galvanomètre à cadre mobile

Posté par
Mac9 25-04-12 à 20:01

Bonsoir,

J'ai un dm d'électromagnétisme à rendre après les vacances et j'aurais besoin d'aide.


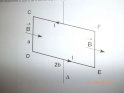
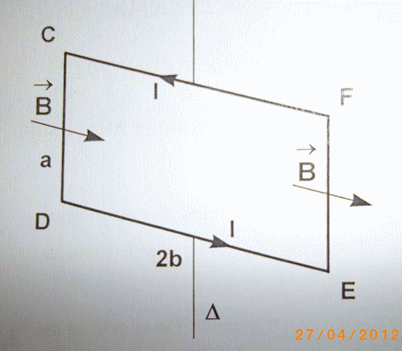
On considère un galvanomètre à champ radial. Le cadre conducteur rectangulaire CDEF, de côté a et 2b, parcouru par un courant d'intensité I, est mobile autour de l'axe .
-Le champ magnétique B, créé par les pièces polaire d'un aimant, est radial et constant en module sur une circonférence de rayon b et d'axe
-Le cadre est maintenu par un fil vertical de constant de torsion C. S'il s'écarte d'un angle ar rapport à une position moyenne, il subit un couple de rappel élastique =C vers cette position/
-R résistance du cadre
-J le moment d'inertie du cadre par rapport à . On supposera que le système est soumis à un amortissement dont le moment par rapport à est (frott)=-f.d/dt.

1) Déterminer la force de Laplace s'exerçant sur chacun des côtés du cadre.
2) En déduire le moment résultant de ces forces par rapport à
3) Montrer, à l'aide du théorème du moment cinétique, que l'équation différentielle du mouvement du cadre est de la forme: Jd2/dt2+fd/dt+C=2abBi(t)=0i(t)
4) Calculer la fem induite e en fonction de d/dt (Trouver la relation entre i(t) et d/dt sachant que i(t) est la somme d'un courant I créé par le générateur extérieur, de résistance interne r et d'un courant créé par la fem e)
5) En déduire l'expression de l'équation différentielle du mouvement du cadre
6) Déterminer la relation liant m et I en régime permanent
7) Montrer que pour obtenir l'équilibre dans un temps minimum, il faut obéir à la condition:
f+4a2b2B2/R+r=2CJ

1) Je sais que dFLa=I.dl^B.
   Le long de CD FLa sera selon i; le long de EF FLa sera selon -i et sur les deux autres côtés FLadevrait être nul

J'aurais besoin d'aide pour résoudre cet exercice. Merci par avance pour toute l'aide que vous m'apporterez.

Posté par
Marc35re : Galvanomètre à cadre mobile 25-04-12 à 22:36

Bonsoir,
Le cadre ne comporte qu'une seule spire ?...
Je pense que la force de Laplace s'exerce sur le côté de longueur a (il doit y avoir un schéma).
Donc la force de Laplace qui s'exerce sur les deux côtés est :
\vec{dF}\,=\,i\,\vec{dl}\,\wedge\,\vec{B}
Donc, pour un côté de longueur a:
F\,=\,i\,a\,B
le sens de \vec{F} étant donné par le produit vectoriel.

Posté par
Phy-Chre : Galvanomètre à cadre mobile 27-04-12 à 15:11

J'ai le même exercice avec les mêmes questions sur lesquelles je bloque, l'enseignant est un peu aller vite... Il s'agit en effet d'un cadre ne comportant qu'une seule spire !

Voici le shéma :

Galvanomètre à cadre mobile

La 1ère réponse me semble correcte, mais je n'arrive pas à voir dans quel sens tourne le cadre... (je ne vois pas très bien l'orientation de B !

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
Phy-Chre : Galvanomètre à cadre mobile 27-04-12 à 15:14

j'espère que vous verrez mieux le schéma :

Galvanomètre à cadre mobile

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
Marc35re : Galvanomètre à cadre mobile 28-04-12 à 14:24

Bonjour,
Pour placer une image sur le serveur de l'île, il faut utiliser l'icône Img sous le cadre de réponse. Il y a quelques restrictions sur la taille de l'image et il vaut mieux utiliser le format gif.
Voir le schéma ci-dessous...
Si ça ne suffit pas, on peut faire une vue de dessus...



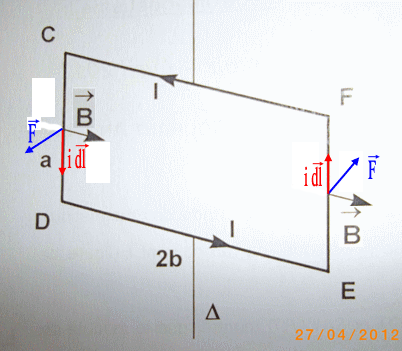
Galvanomètre à cadre mobile

Posté par
Marc35re : Galvanomètre à cadre mobile 28-04-12 à 19:53

Citation :
je ne vois pas très bien l'orientation de B !

B est radial donc perpendiculaire aux côtés CD et FE, donc orthogonal à  i\,\vec{dl}  .

Posté par
Phy-Chre : Galvanomètre à cadre mobile 28-04-12 à 22:50

Pour la 1ère question il faut trouver : F(CF) = F(DE) = 0
et F(CD)= - F(CF) = I*B*A non ?

Posté par
Marc35re : Galvanomètre à cadre mobile 29-04-12 à 12:10

F(CF) = F(DE) = 0 ==> oui parce que   I\vec{dl}   et  \vec{B}  sont colinéaires
F(CD)= - F(EF) = I a B  comme je l'ai écrit dans le message "Posté le 25-04-12 à 22:36".
C'est deux forces forment un couple. Elles sont séparées de 2b donc le moment est facile à calculer.

Posté par
Phy-Chre : Galvanomètre à cadre mobile 30-04-12 à 09:29

Pour la deuxième question, je dirais en considérant le point A comme étant le point d'application de la force et 0 le centre du système :

M(F[CD]) = OAF[CD] = -b*I*B*a

M(F[FE])= FEF[FE] = b*I*B*a

les deux autres moments sont nuls car F = 0, et donc la somme des moments est égale à M(F[CD])+M(F[FE])=0

est-ce ça ? par contre pour les questions qui suivent je ne comprends pas grand chose...

Posté par
Marc35re : Galvanomètre à cadre mobile 30-04-12 à 12:05

Oui, à part les signes... parce que la somme des moments est nulle, ce qui est ennuyeux...
M_{F_{CD}}\,=\,\vec{OC}\wedge \vec{F}\,=\,baIB\vec{k}
M_{F_{EF}}\,=\,\vec{OF}\wedge \vec{F}\,=\,baIB\vec{k}
Le produit vectoriel dans les deux cas donne un vecteur orienté vers le haut.
M_{F_{CD}}\,+\,M_{F_{EF}}\,=\,2baIB\vec{k}

Posté par
Marc35re : Galvanomètre à cadre mobile 30-04-12 à 12:13

Pour la 3, tu connais le théorème du moment cinétique ?
\frac{d\vec{L}}{dt}\,=\,\Sigma\,\vec{M_F}

Posté par
Phy-Chre : Galvanomètre à cadre mobile 01-05-12 à 13:21

Dans la partie de droite j'ai M(F[CD]) + M(F[EF]) + (-f.d/dt) par contre à gauche je ne vois pas comment trouver le Jd2/dt2 et le C...

Pour la question 4) on sait que e = i(t) * (R+r) soit i(t) = e / (R+r) si on a le e, on peut exprimer i(t) en fonction de d/dt

Je ne suis pas sûr mais d'après la loi de Lenz on obtient e = -B*a*b*d(t)/dt

Pour la question 5) on remplace le i(t) dans l'équation différentielle

Est-ce bon ? (Pour la question 3 j'ai beau faire mes calculs je ne trouve pas le C...)

Posté par
Marc35re : Galvanomètre à cadre mobile 01-05-12 à 15:50

On va s'occuper de la 3 d'abord...
\frac{d\vec{L}}{dt}\,=\,\Sigma\,\vec{M_F}
\vec{L}\,=\,\vec{r}\wedge\vec{p}\,=\,\Sigma_i\left(\vec{r_i}\wedge m_i\vec{v_i}\right)
Mais  \vec{v_i}  est la vitesse tangentielle (rotation du cadre).
\large \vec{v_i}\,=\,r_i\frac{d\theta}{dt}\,\vec{e_{\theta}}
\vec{L}\,=\,\Sigma_i\,\left(\vec{r_i}\wedge mr_i\frac{d\theta}{dt}\,\vec{e_{\theta}}\right)\,=\,\Sigma_i\,\left(m_ir_i^2\right)\,\frac{d\theta}{dt}\,\vec{e_z}
On pose :
J_{\Delta}\,=\,\Sigma_i\,\left(m_ir_i^2\right)
Donc :
\large \frac{d\vec{L}}{dt}\,=\,J_{\Delta}\,\frac{d^2\theta}{dt^2}\,\vec{e_z}
La somme des moments des forces :
\large \Sigma\,\vec{M_F}\,=\,\left(2abIB\,-\,\textrm{f}\,\frac{d\theta}{dt}\,-\,C\theta\right)\,\vec{e_z}
2abIB  : moment des forces calculé précédemment
-\,\textrm{f}\,\frac{d\theta}{dt}  : moment de la force de frottement (donné dans l'énoncé)
-\,C\theta  :  moment du couple de torsion dû au fil de suspension
Donc :
\large J_{\Delta}\,\frac{d^2\theta}{dt^2}\,\vec{e_z}\,=\,\left(2abIB\,-\,\textrm{f}\,\frac{d\theta}{dt}\,-\,C\theta\right)\,\vec{e_z}
D'où :
\large J_{\Delta}\,\frac{d^2\theta}{dt^2}\,+\,\textrm{f}\,\frac{d\theta}{dt}\,+\,C\theta\,=\,2abIB
D'autre part :
\Phi_0\,=\,\vec{B}.\vec{S}\,=\,2ba\,B
Donc :
2ba\,B\,I\,=\,\Phi_0\,I

( J'ai appelé  \vec{e_z}  le vecteur unitaire que tu as dû appeler  \vec{k} )

Posté par
Marc35re : Galvanomètre à cadre mobile 01-05-12 à 16:04

Pour la 4
L'équation de la maille peut s'écrire :
e\,-\,e_i(t)\,-\,(R+r)i(t)\,=\,0
\large i(t)\,=\,\frac{e\,-\,e_i(t)}{R+r}
On a, comme tu l'as écrit, la fem induite :  \large e_i(t)\,=\,Bab\frac{d\theta}{dt}
Donc :
\large i(t)\,=\,\frac{e}{R+r}\,-\,\frac{Bab}{R+r}\frac{d\theta}{dt}

Posté par
Marc35re : Galvanomètre à cadre mobile 01-05-12 à 16:10

Pour la 5
Comme tu l'as écrit, on remplace I par i(t) dans l'équation différentielle.

\large J_{\Delta}\,\frac{d^2\theta}{dt^2}\,+\,\textrm{f}\,\frac{d\theta}{dt}\,+\,C\theta\,=\,2abB\,\left(\frac{e}{R+r}\,-\,\frac{Bab}{R+r}\frac{d\theta}{dt}\right)
\large J_{\Delta}\,\frac{d^2\theta}{dt^2}\,+\,\left(\textrm{f}+2\frac{(Bab)^2}{R+r}\frac{d\theta}{dt}\right)\,\frac{d\theta}{dt}\,+\,C\theta\,=\,2abB\,\frac{e}{R+r}

Posté par
Phy-Chre : Galvanomètre à cadre mobile 01-05-12 à 18:01

Pour la fem induite, nous avons trouvé le même résultat au signe près, je m'étais trompé de signe ? Je comprends mieux d'où vient le C maintenant, je ne l'avais tout bonnement pas considéré comme un moment, c'est pour cela qu'il n'apparaissait pas dans mon équation !

Pour la question 6, puisque nous sommes en régime permanent, les dérivées première et seconde de sont nulles, ils suffit donc uniquement d'isoler pour trouver m en fonction de I.

Pour la dernière question il faut se servir de la question 6 n'est-ce pas ?

Posté par
Marc35re : Galvanomètre à cadre mobile 01-05-12 à 19:47

Citation :
Pour la fem induite, nous avons trouvé le même résultat au signe près, je m'étais trompé de signe ?

Il faut se méfier du signe de la fem induite. Le signe - signifie simplement qu'elle s'oppose au phénomène qu'il l'a produite.
C'est la loi de Lenz que l'on peut énoncer : "Le courant induit est tel qu'il s'oppose à la variation du flux inducteur".
C'est le courant induit dont on peut déterminer le sens. La fem induite est telle qu'elle fait circuler le courant induit dans ce sens-là.
Ce qui est sûr, c'est que la fem induite s'oppose à la fem extérieure parce qu'elle tend à faire circuler un courant en sens inverse du courant fourni par la fem extérieure.
C'est ce que tente de montrer les deux schémas joints selon l'orientation choisie pour les tensions.

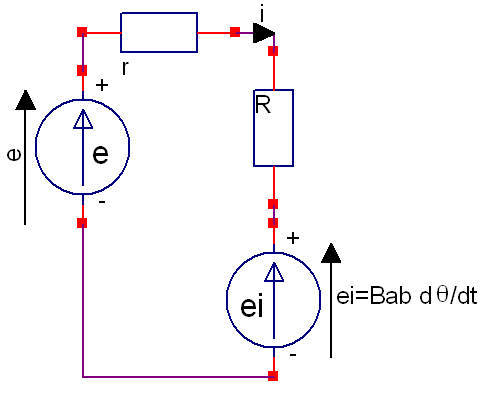
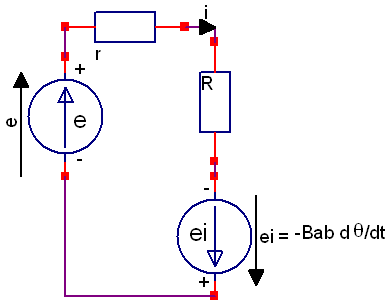
Galvanomètre à cadre mobile

Galvanomètre à cadre mobile

Posté par
Marc35re : Galvanomètre à cadre mobile 01-05-12 à 20:19

Citation :
Pour la question 6, puisque nous sommes en régime permanent, les dérivées première et seconde de sont nulles, ils suffit donc uniquement d'isoler pour trouver m en fonction de I.

Exact...
Citation :
Pour la dernière question, il faut se servir de la question 6 n'est-ce pas ?

La question 6 n'apportera pas grand-chose pour cela.
La question 6 donne la déviation permanente en fonction de I (permanent).
La réponse à la question 7 est ce qu'on appelle le régime apériodique critique.
Pour résoudre une telle équation, il faut résoudre l'équation caractéristique qui est une équation du second degré. Le discriminant peut être positif, nul ou négatif.
Le discriminant positif correspond à un régime amorti sans oscillation.
Le discriminant négatif correspond à un régime amorti avec oscillations.
Le discriminant nul correspond au régime limite entre les deux. C'est un régime amorti sans oscillation mais qui arrive le plus rapidement à la position d'équilibre.

Citation :
f+4a2b2B2/R+r=2CJ

Je ne suis pas d'accord avec le 4

Posté par
Marc35re : Galvanomètre à cadre mobile 01-05-12 à 20:41

Il y a une petite erreur...

Citation :
On a, comme tu l'as écrit, la fem induite :  \large e_i(t)\,=\,Bab\frac{d\theta}{dt}

C'est exact mais il y a une fem induite dans les deux barres verticales donc la fem induite totale est
\large e_i(t)\,=\,2Bab\frac{d\theta}{dt}
Donc :
\large i(t)\,=\,\frac{e}{R+r}\,-\,\frac{2Bab}{R+r}\frac{d\theta}{dt}
D'où l'équation différentielle :
\large J_{\Delta}\,\frac{d^2\theta}{dt^2}\,+\,\textrm{f}\,\frac{d\theta}{dt}\,+\,C\theta\,=\,2abB\,\left(\frac{e}{R+r}\,-\,\frac{2Bab}{R+r}\frac{d\theta}{dt}\right)
\large J_{\Delta}\,\frac{d^2\theta}{dt^2}\,+\,\left(\textrm{f}+4\frac{(Bab)^2}{R+r}\frac{d\theta}{dt}\right)\,\frac{d\theta}{dt}\,+\,C\theta\,=\,2abB\,\frac{e}{R+r}
Et là, je suis d'accord avec la réponse proposée dans la question 7.

Posté par
Mac9re : Galvanomètre à cadre mobile 02-05-12 à 21:17

Merci infiniment pour toute cette aide, cela a grandement facilité la compréhension de cet exercice.

Posté par
Phy-Chre : Galvanomètre à cadre mobile 03-05-12 à 12:37

Je vous remercie également, je pense que si on me repose un exercice du même type je serai capable de le refaire !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !