Inscription / Connexion Nouveau Sujet
Freinage d'une spire par induction
Bonsoir, j'ai un petit exercice sur le freinage d'une spire par induction..
J'ai un peu du mal avec l'électromagnétisme 
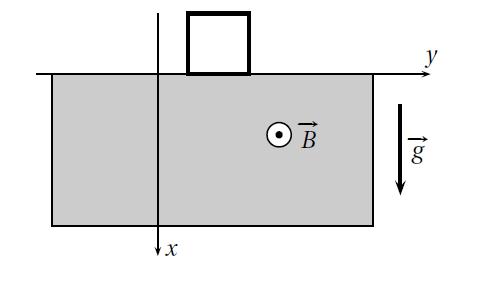
Une spire carrée de côté a, de masse m, tombe dans le champ de pesanteur "vecteur g"=g*"vecteur Ux". Dans le demi espace x>0 règne le champ magnétique uniforme et permanent "vecteur B"=B0*"vecteur Uz". A l'instant t=0, la spire se trouve dans la situation sur la figure ci-contre, et sa vitesse est "vecteur V"= V0*"vecteur Ux", son côté est en x=0.
1) Montrer que le mouvement ultérieur de la spire reste une translation verticale selon l'axe.
2) Soit R la résistance de la spire. Déterminer la vitesse V(t) de la spire.
1)je vois pas comment on peux démontrer cela
2) quel formule utiliser s'il vous plais ? 
Quelle est l'intensité du courant induit dans la spire par la variation du flux magnétique la traversant? (Loi de Lenz)
Quelle est la force s'exerçant en conséquence sur le cadre? (Laplace)
merci =) j'irai plancher sur cette aide.
j'ai une autre question..
3) La spire a maintenant une résistance nulle (spire supraconductrice) et on note L son inductance propre. Reprendre l'étude précédente et préciser la condition d'oscillation de la spire..
une idée sur quoi démarrer ? :$
merci à vous..
1)
Le courant induit dans la spire est évidemment le même dans toute la spire.
a)
Lorsque la spire est entièrement dans le champ magnétique :
Avec la règle des 3 doigts de la main qu'il faut ... :
Les forces sur les brins horizontaux sont verticaux, de même norme mais de sens opposés --> pas d'influence sur le mouvement vertical de la spire
Les forces sur les brins verticaux sont horizontaux, de mêmes normes, de même direction (qui est celle de Oy) mais de sens opposés. --> pas d'influence sur le mouvement vertical de la spire.
b) lorsque la spire n'est pas entièrement dans le champ magnétique :
Avec la règle des 3 doigts de la main qu'il faut ... :
La force sur le brin horizontal hors du champ magnétique est nul.
La force sur le brin horizontal dans le champ magnétique est vertical --> pas de modification dans la direction vertical du mouvement de la spire.
Les forces sur les parties des brins verticaux hors du champ magnétique sont nuls.
Les forces sur les parties des brins verticaux dans le champ magnétique sont horizontaux, de mêmes normes, de même direction (qui est celle de Oy) mais de sens opposés. --> pas d'influence sur le mouvement vertical de la spire.
-----
Sauf distracion. 
Merci J-P mais suffirait il de faire un bilan des forces: le poids et les forces de La place en appliquant la loi de Lenz ?
on condisererai le cas de la spire dans un champ B ou hors du champ :
Le poids est celui Ux dans les deux cas
à l'aide de la main droite on montre que les force sont selon le vecteur Ux.
est ce bon ?
2)Pour déterminer la vitesse quel formule utiliser ?
la force de Lorentz mais je ne l'ai pas...
on condisererai le cas de la spire dans un champ B ou hors du champ : ...
Il faut aussi considérer le cas de la spire partiellement dans le champ B ...

merci. c'était pour la question 1, j'avais mal lu.
on considère aussi la spire partiellement dans le champ.
Quel raisonnement peut-on faire sur les forces de laplace ? on sait qu'il seront le vecteur Ux mais comment justifier proprement...
Merci à toi..
2)
e = -dPhi/dt
dPhi/dt = 0 si la prise en entièrement hors du champs B ou est entièrement dans le champ B.
--> il faut étudier ce qui se passe pendant que la spire entre (ou sort) du champ B.
dPhi = B.dS
dPhi/dt = B.dS/dt = B.a.dx/dt
---
e = -dPhi/dt
e = -B.a.dx/dt
i = e/R
i = -(B.a/R).dx/dt
Et (voir ma réponse précédente) , il suffit de déterminer la force de Laplace qui agit sur le brin horizontal de la boucle qui est dans le champ B (fonction du temps).
Et on pourra alors écrire l'équation différentielle donnant x en fonction du temps (limité à l'intervalle de temps pendant lequel la spire n'est pas entièrement dans le champ B).
vecteur(Poids) + vecteur(Force de Laplace trouvée ci-dessus) = m . vecteur(accélération)
Tous ces vecteurs étant verticaux.
-----
Sauf distraction ou bêtise de ma part. 
Merci cela me permet de verifier mes calcules.
il me manquer enfaite juste cette idée de transformer dS en dS=L*dl=L*dv/dt ...
ok après je fais un petit schémas pour montrer que Idl est selon le vecteur Uy puisqu'on connais B je fais mon produit vectoriel pour trouver que c'est selon Ux
on projet sur Ux et on a:
m*g - B².a/R*dv/dt=m*d²v/dt² => g = d²v/dt² + B².a/(R.m)*dv/dt
Il me reste une question J-P:
3) La spire a maintenant une résistance nulle (spire supraconductrice) et on note L son inductance propre. Reprendre l'étude précédente et préciser la condition d'oscillation de la spire..
question qui me rappelle ma chère terminal ^^.
On cherche une équation differentielle à l'aide du théoreme du moment cinétique je pense avec une condition sur téta.
non ?
Si la spire est inductive au lieu de résistive, alors on remplace e = R.i par e = L.di/dt dans le raisonnement.
Sauf distraction. 
petite question:
lorsque je souhaite déterminer l'expression de la force de Laplace j'ai:
F=idl*Uy ^ B*Uz or dl=dx et là j'ai un probleme dans mon expréssion i*dl car si oui
i*dl=B*a*dx²/dt ... probleme..
F = BIL.sin(alpha) (Avec F la force de Laplace)
Ici (sur un brin horizontal dans le champ B, alpha = 90°) : F = B.i.a
Cas à spire résistive : F = B*(-(B.a/R).dx/dt).a = -(a²B²/R) dx/dt
--> Equation différentielle :
mg - (a²B²/R) dx/dt = m.d²x/dt².
-----
Sauf distraction ou erreur. 
pour la question 3:
j'ai e=L*di/dt soit i = e*t/L
soir F(laplace)= i.a.sin(téta).B
PDF sur la spire inductive et projection sur Ux:
mg- B².a.sin(téta).t/L.dx/vt=m*d²v/dt² et on pose dx/dt=v(t)
soit g= dv(t)/dt + (B².a.sin(téta).t)*v(t)/m
est ce bon ?
et pourquoi on ne considère pas un brin vertical ?
Comme je l'ai déjà écrit plusieurs fois :
Les forces sur les parties des brins verticaux dans le champ magnétique sont horizontaux, de mêmes normes, de même direction (qui est celle de Oy) mais de sens opposés. --> pas d'influence sur le mouvement vertical de la spire.

Oui c'est vrai pardon  ..
..
et en ce que concerne mon equation differentiel, est elle juste à votre avis ?
Spire inductive :
e = -B.a.dx/dt
e = L.di/dt
-B.a.dx/dt = L.di/dt
di/dt = -(B/L).a.dx/dt
i = -(B/L).a.x + K
en t = 0 (juste avant que le spire n'entre dans le champ B) : x = 0 et i = 0
--> i = -(B/L).a.x
F = BIa = -(B²/L).a².x (Force de Laplace ... tant que la spire n'est pas entièrement dans le champ B).
...
-----
Sauf distraction ou erreur. 
ok j'arrive a g= d²x/dt² + b².a².x/(L*m)
on a une équation differentielle du second ordre avec second menbre constant.. mais la condition elle sera sur x ?
A supposer qu'il n'y ait pas d'erreur dans tout ce qui a été fait (ce que je n'ai pas vérifié), il faut maintenant trouver l'expression de x(t) en résolvant l'équation différentielle et en tenant ensuite compre que x(0) = 0 et (dx/dt)(0) = Vo.
Il restera ensuite à trouver le max de x(t) (qui correspond au niveau le plus bas atteint par le coté horizontal du bas de la spire).
Ce max sera atteint au premier passage par 0 de dx/dt.
Et la spire ne pourra pas à cet instant être toute dans le champ B.
--> il faut exprimer les conditions (sur les paramètres Vo, m, a , B, L) pour que x max < a
Sauf distraction ou erreur. 


