Inscription / Connexion Nouveau Sujet
formation des nuages
Bonsoir,
J'ai des difficultés avec les premières questions d'un exercice de thermodynamique. J'ai passé beaucoup de temps dessus mais je reste vraiment bloquée et cela m'empêche de faire les questions suivantes.
Voici l'énoncé en question :
Soit un système constitué de no moles d'un corps pur (l'eau en l'occurence) dans l'état gazeux, à la température To et à la pression Po. On suppose que se forme en son sein une gouttelette d'eau liquide sphérique de rayon r contenant n moles avec n très petit devant no.
On admet que la pression au sein de la gouttelette Pl satisfait la loi de Laplace : Pl=Po+2
/r où correspond à la constante de tension superficielle liquide-gaz, dont on néglige toute dépendance vis-à-vis de la pression ou de la température. L'équilibre mécanique et thermique est supposé être satisfait à tout instant.
Pour un système évoluant entre deux états d'équilibre, l'état initial i et l'état final f, en contact avec un thermostat(de température To) et un réservoir de volume (qui fixe donc la pression à Po) on a : 
U+PoV-ToS
0 qui établit que G*=U-ToS+PoV est le potentiel thermodynamique à considérer dans la situation d'un système en contact avec un thermostat et un réservoir de volume, i.e pour une transformation monotherme monobare.
1. Déterminer la variation G* correpondant à la transformation monotherme monobare amenant une goutte d'eau initialement sous forme gazeuse(de volume Vg à la température To et à la pression Po) à devenir liquide (de volume Vl, à la température To et à la pression Pl). Le résultat fera apparaître les énergies libres de la phase liquide Fl et de la phase gazeuse Fg, ainsi que les volumes de chacune de ces phases. Chacun des termes devra faire apparaître les variables dont il dépend.
2. Réexprimer G* à l'aide des enthalpies libres de chacune des phases ainsi que du volume de la phase liquide (et seulement celui-là). A nouveau, chacun des termes devra faire apparaître les variables dont il dépend.
3. Prendre en compte la tension superficielle amène à ajouter un terme de la forme S où S désigne la surface de la goutte (supposée sphérique). La variation du potentiel thermodynamique G* prend alors la forme suivante :
G*=Gl(To,Pl,n)-Gg(To,Po,n)+(Po-Pl)V1(To,Pl,n)+S
a) Justifier que dans la limite , l'expression précédente se réécrit :
G*=n(gl(To,Po)-gg(To,Po))+S
Voici ce que j'ai fait :
1. G=U+PV-TS=PV+F
Donc G*=PoVg+Fg-PlVl+Fl
Le problème c'est qu'il manque To car je pense qu'il faut le mettre vu que l'énoncé dit :"Chacun des termes devra faire apparaître les variables dont il dépend" et G dépend de To
2.Gg-Gl=Ug-ToSg+PoVg-Ul+ToSl-PlVl
Comme l'expression de la question 3 est G*=Gl(To,Pl,n)-Gg(To,Po,n)+(Po-Pl)V1(To,Pl,n)+S j'ai cherché à faire apparaître (Po-Pl)V1(To,Pl,n) mais je ne sais pas si c'est qu'il faut faire et j'ai en utilisant le 1er principe :
Gg-Gl=Q+To(Sl-Sg)+(Po-Pl)Vl
mais ensuite je n'arrive pas à simplifier Q+To(Sl-Sg) pour trouver un résultat convenable.
3.a) Je sais que cette question est censée être simple mais je n'y arrive pas non plus : je n'arrive pas à simplifier pour montrer que le terme (Po-Pl)Vl(To,Pl,n) est négligeable devant Gl(To,Pl,n)-Gg(To,Po,n)+
S
Merci d'avance pour votre aide !
Bonjour
J'ai traîné à répondre car je ne suis pas très à l'aise avec cet énoncé : outre les notations erronées ou ambiguës, je ne comprends pas vraiment l'objectif final.
J'ai rectifié par moi-même la définition fausse du potentiel thermodynamique. Je pense qu'il faut lire :
G*=U-ToS+PoV
Il est maladroit d'utiliser la même lettre "S" pour désigner l'entropie et l'aire de la surface. Pourquoi pas la lettre A pour l'aire de la surface délimitant la goutte d'eau.
Sinon :
* Je pense que la température To doit être considérée comme une donnée du problème ; la température étant fixe au cours de l'évolution.
* L'évolution étant considérée comme réversible du point de vue thermique :
Q=To.S
* Pour la question 3 : la loi de Laplace conduit à :
Par ailleurs :
???
Tu as une étude plus rigoureuse du phénomène ici : partie5 : Microphysique des nuages
Dans ce contexte, le potentiel chimique (noté µ dans le document) se confond avec l'enthalpie libre molaire noté "g" dans ton énoncé.
Bonsoir,
Merci de ta réponse. J'ai essayé de prendre compte de tes remarques pour avancer :
Dans la question 2, j'ai G*=2To(Sl-Sg)+(Po-P1)Vl
Est-ce que tu penses que c'est le bon résultat ? Ca me semble bizarre vu le G* donné à la question 4.
Question 4 : Du coup on a G*=Gl(To,Pl,n)-Gg(To,Po,n)+1/3 S mais je ne vois pas comment cela permet de conclure pour trouver le résultat attendu.
Voici une démonstration possible des deux dernières questions. Sous toute réserve sans connaître l'intégralité de l'énoncé et le but recherché dans ce problème...
Je pars de l'expression apparemment fournie par l'énoncé que je considère comme correcte :
L'enthalpie libre étant une grandeur extensive, la phase gazeuse étant homogène :
Propriété de l'enthalpie libre d'un corps pur comme l'eau à l'état liquide :
Le calcul de l'intégrale se faisant à n et à To fixes. Dans ses conditions (voir cours sur les propriétés de G) :
(volume des n moles de liquide à la température To)
Si on suppose la variation relative de pression faible (), on peut considérer le volume du liquide comme indépendant de la pression. Ce qui conduit à :
D'où l'expression :
L'enthalpie libre de la phase liquide étant aussi une fonction extensive, on obtient l'expression proposée :
Ok j'ai compris le raisonnement mais par contre j'ai un petit problème : la formule n'est pas dans mon cours mais ça me fait penser un peu à ce qu'on a pour le potentiel chimique. Est-ce qu'il n'y a pas un autre moyen de répondre à cette question ou par analogie avec ce qu'on fait pour le potentiel chimique de trouver cette expression ?
Je donne la suite de l'énoncé :
3.b) En déduire que G* s'écrit sous la forme d'un polynôme cubique en fonction du rayon r de la goutte.
c) Tracer schématiquement G*(r) en fonction de r et selon le signe de gl(To,Po)-gg(To,Po)
En déduire l'état stable correspondant du système.
d) Dans le cas où l'état stable correspond à la phase liquide, qualifier l'état corespondant à r=0. Justifier le fait que la goutte d'eau ne peut croître que si la taille du germe initial dépasse une valeur critique rc dont on donnera l'expression en fonction de la différence des enthalpies libres molaires
e) Proposer un processus permettant de faciliter la formation de tels germes.
Pour la question b) je ne sais pas s'il faut exprimer gl(To,Po)-gg(To,Po) en fonction de r sinon ça donne : n(gl(To,Po)-gg(To,Po))+
4/3 
r3.
Pour la c) si on a une forme du style a3+b on a une courbe de fonction cubique. L'état stable est celui pour lequel on a
Pour le reste je ne vois pas trop pour le moment.
Concernant la démo : dans le cas d'un corps pur dans une phase donnée, le potentiel chimique est égal à l'enthalpie libre molaire.
À n fixe pour un corps pur dans une phase donnée, la troisième identité thermodynamique est sans doute à ton programme :
dG =V.dP -S.dT
Donc à n et T fixes, V=....
Pour la suite :
n est proportionnel au volume de la goutte donc au cube de son rayon.
S est proportionnelle au carré du rayon.
Bonsoir,
Ok merci pour la démo je pense que c'est bon. Par contre j'ai dû mal à comprendre pourquoi si ça signifie d'une part que la variation relative de pression est faible et d'autre part je ne comprends pas pourquoi ça signifie qu'on peut considérer le volume du liquide comme indépendant de la pression. Je veux bien que tu me réexpliques stp.
Pour la 3 b) j'ai n(gl(To,Po)-gg(To,Po))+(Pl-Po)2/3 r3 trouvé à partir de l'expression de donné dans l'énoncé et de S=4r2
mais il y a 2 problèmes :
- on ne connaît pas le signe de Pl-Po
- on peut exprimer n=CV=4/3C r3 mais ensuite on aura une nouvelle grandeur C qui ne s'exprime pas avec les données du problème donc je ne sais pas si c'est pertinent.
Il s'agit bien de la variation de pression divisée par la pression initiale. C'est ce qu'on appelle la variation relative de pression. Contrairement à un gaz, un liquide est très peu compressible. On peut donc considérer que, à température fixe et à quantité de matière fixe, le volume du liquide est indépendant de la pression. Il peut être considéré comme constant lors du calcul intégral.
Ce que tu fais ensuite est maladroit. Tout simplement, avec les notations habituelles :
Cela peut s'écrire :
où B est une constante positive et A une constante dont le signe est celui de .
Si :
fonction monotone croissante de r ;
si :
présente un maximum pour une valeur particulière rc de r. Sachant que, à Po et To fixes, G* ne peut que décroître... Je te laisse réfléchir. Tu devrait retrouver une propriété connue du potentiel chimique puis montrer la nécessité de germes de rayon supérieur à rc...
Courbe verte :
Courbe rouge :
courbe bleue :
échelle totalement arbitraire.
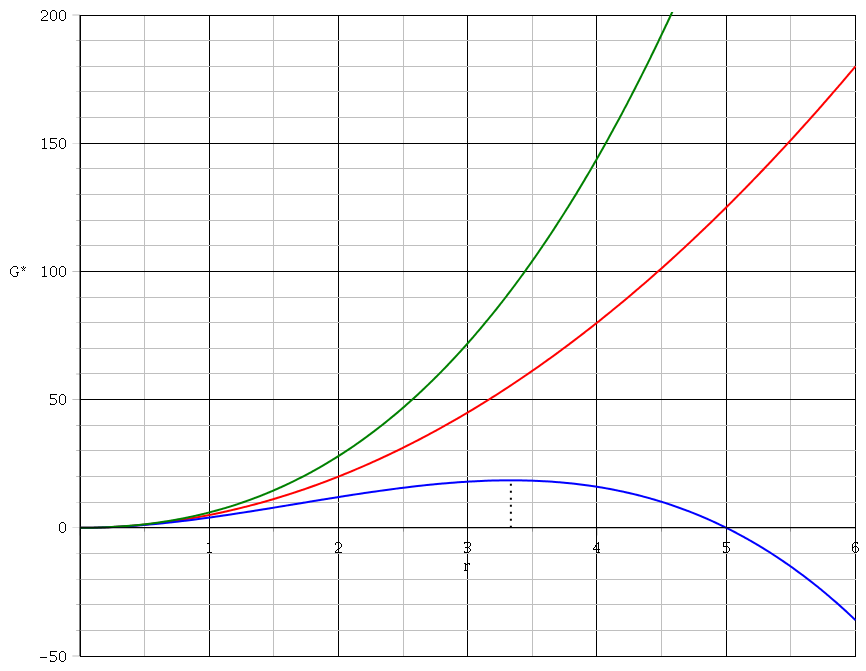
Bonsoir,
Merci bcp pour ton aide. Je pense que j'ai compris. Je regarderai les autres questions demain soir.
Bonsoir,
Il y a quelque chose que je ne comprends pas : pourquoi on ne remplace pas vu qu'il dépend de r?
d) Pour la courbe bleu on voit que il y a un maxima en un point r=rc. Ce point représente l'état instable du système. Sachant que le G est un potentiel thermodynamique, il ne peut que diminuer donc le rayon augmente (déplacement de r à la droite de rc). Est-ce que c'est cela ? Et rc correspond à la valeur telle que d(G(r)*/dr=0
Reprends ton cours sur la notion de tension superficielle : tu verras que est une constante caractéristique du liquide. Cela est d'ailleurs rappelé en début d'énoncé.
Pour b), il faut distinguer deux cas :
1° : les conditions de température et de pression sont telles que :
Le minimum de G* correspond à r=0 c'est à dire à l'absence de liquide. On peut aussi imaginer un état initial où serait présente une goutte de liquide de rayon r quelconque ; le système évoluerait spontanément dans le sens de G* décroissant donc dans le sens de r décroissant, donc dans le sens de disparition du liquide. Tu retrouve là une propriétés importante du potentiel chimique : lors d'un changement d'état, la matière passe spontanément de la phase où le potentiel chimique est le plus grand vers la phase où le potentiel chimique est le plus faible. Cela justifie d'ailleurs l'appellation "potentiel chimique" par analogie avec le sens conventionnel du courant qui , dans un conducteur, circule du potentiel électrique le plus élevé vers le potentiel le plus faible.
2° :
Cette situation correspond logiquement à une température et une pression telles que l'état stable est l'état liquide. C'est vrai mais la tension superficielle complique un peu la situation. Imagine une goutte de liquide telle que r<rc. Elle évolue vers r=0 : cette goutte est instable. Imagine au contraire une impureté (poussière...) de rayon supérieur à rc. L'apparition de liquide autour de ce germe produit une goutte dont le rayon va croître spontanément puisque G* va diminuer quant r va augmenter. Quand l'inégalité précédente sur les potentiels chimiques est satisfaite sans la présence de germe permettant l'apparition de liquide, on dit que la vapeur d'eau est dans un état métastable.
Juste une remarque : je sais bien qu'il est fastidieux de copier l'énoncé sur le forum mais, si tu avais fourni la question 3 dès le début, j'aurais tout de suite compris l'objectif de l'exercice et mon aide aurait sans doute été plus efficace ! 
Annuler
connectez vous