Inscription / Connexion Nouveau Sujet
forces et statique
bonsoir
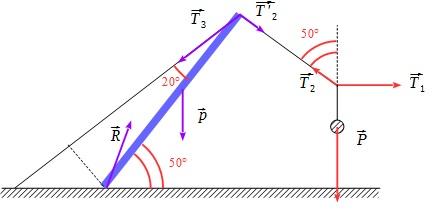
trouver T1. T2.T3 pour le mecanisme représenté sur la figure suivante sachant que la poutre est homogéne et que son poids est de 800N ? le poids suspendu en A est de 2000 N
Re-bonjour Ahlambebe.
Pour pouvoir répondre, il faudrait éclaircir un peu ce qui concerne le mécanisme : il y a là dedans des fils et des parties rigides (poutre(s)).
La difficulté vient de ce qu'on ne voit pas trop ce qui est fil et ce qui est poutre.
Précisions attendues en vue d'une réponse !
A plus.
bonj
il ya trois cables
la poutre fait une angle de 90° avec T2
T2 est en relation avec T1et le poid 2
la poutre fait une angle de 50° avec le sol et 20° avec T3
lorseque on decompose T2
t2x=T1 ET T2Y=P T1= t2cos 40°
T1 DONC=t2 cos40°
t2y=t2sin40°=p
t2=p/sin40°= 2000/sin 40° = 3125N
T1= 3125cos40°=2393 N
lorseque on decompose p
px=pcos50°
py=psin50°
on decopose t3 sur la poutre
t3x=t3cos 20°
t3y=t3sin20°
fx=o
t3x+px=0 t3x=-px =-pcos50° = -800cos50°= 514.23 N
t3=t3x/cos20= 574 N
fy=0
py+t3y+t2=0
D'accord, j'y vois plus clair.
Il faut étudier séparément l'équilibre de la charge suspendue en A et l'équilibre de la poutre.
Pour la charge suspendue en A :
Soit :
Par projection sur la verticale (sens + vers le haut), on obtient : çàd :
et donc
Par projection sur l'horizontale (sens + vers la droite) : çàd :
Numériquement, j'obtiens : et
C'est également ce que vous avez obtenu.
Je poste cette partie et je m'intéresse à la poutre ensuite...
A suivre.
Suite et fin.
Pour la poutre : axe au point de contact de la poutre avec le sol, sens + = sens des aiguilles d'une montre.
En exprimant chaque moment :
En divisant par et en isolant
:
Numériquement : et
Vous devez revoir votre calcul, il n'est pas correct car vous n'avez pas tenu compte de la réaction de l'axe sur mon schéma.
Au revoir.