si ca l'mage

Bonjour.

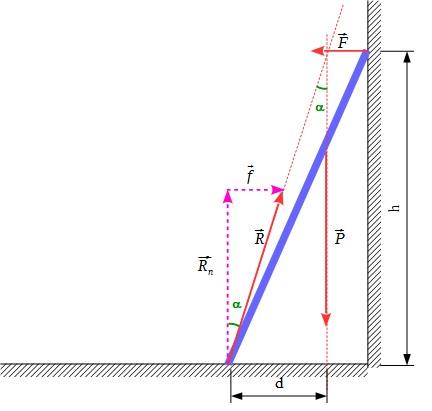
Le système {échelle ; personne} est soumis à 3 forces : le poids , la force exercée par le mur (perpendiculaire au mur puiqu'il n'y a pas de frottement) et la réaction du sol (qui peut se décomposer en ses composantes normale et tangentielle ).

Ces trois forces doivent être coplanaires, concourantes et de somme nulle.

Un schéma soigné est une aide précieuse à la résolution qui ne présente plus alors de difficultés insurmontables.

A vous.

bonj
merci picard
u=f/Rn=p/d
donc d=p/u avant le glissement

bonj
je sais comment trouver l'angle mais la distance horizontale d me fait un probleme
dans l'angle on utiluse la premiere equation Fx= 0

slt
le R est que je dois la decomposer sur le plancher?

slt picard
j'utiluse le plancher comme axe horizontale

la distance d a une relation avec quoi ?

selon l'axe des x on a
F-f=o
selon l'axe des y on a
p-Rn=0
f+p.d -Rn.ab=0 ( on vecteurs)

Situation à la limite de glissement :



Moment des forces autour de P :

P * d - R * h = 0 (à la limite de glissement)

R = P * d/h

µ.N = P * d/h
µ.N = N * d/h

d/h = µ

d = µ.h
-----
Sauf distraction.  

merci j-p
mais comment tu connais que p*d-r*h=0 ?
si j'utilise les forces des apuis=0 je sais pas comment je continier

On peut aussi s'en sortir sans passer par les moments.

D'une part :     tan = f/R_n = F/P
d'autre part :    tan = d/h

     f/R_n = d/h
et comme     f/R_n = µ

µ = d/h = F/P

comment tu trouve ca ou est l'angle entre d et h
u=d/h ??? je comprend pas ca

est qui ilya des regles sur le glissement ? je comprend pas la 1ere methodes

p*d mais R*ab ou h ??

aaa sayi merci bcp

si on passe par les moments le h si pas une distance il est vertical mais le d est horizontal et le p est vertical et le f est horizontale est ce que ce nest pas important?

je veux une explication svp

on a comme definition le moment d'une force . par rapport a un point de référence . est le rusultat du produit vectoriel du vecteur joignant ce point de référence au point d'application de la force avec le vecteur force

dans ce cas h est le bras de levier de F

pourquoi le moint avec R ils sont pas au sens contraires les forces quel signe t'utiluse

aa oki
on a pas siter un seul axe dans les moment on peut changer pas decomposer comme les forces

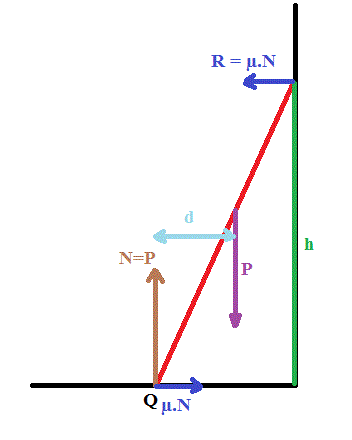
Je prends mes notations.

Par rapport au point situé au pied l'échelle :

h est le bras de levier pour la force R
d est le bras de levier pour la force P
Le bras de levier pour les forces N et µN est nul (puisque les droites d'action de ces forces passe par Q)

La force R à tendance à faire tourner l'échelle autour de Q dans le sens inverse des aiguilles d'une montre
Et donc le moment de la force R par rapport au point Q est M1 = R * h

La force P à tendance à faire tourner l'échelle autour de Q dans le sens des aiguilles d'une montre
Et donc le moment de la force P par rapport au point Q est M2 = - P * d

Le moment des forces N et µN autour de Q sont nuls (puisque bras de levier = 0)

Donc le moment résultant de toutes les forces par rapport au point  est : M = M1 + M2 = R.h - P.d

Et comme l'échelle ne pivote pas autour de Q, c'est que M = 0

---> R.h - P.d = 0
-----

Or, par la première partie de l'exercice (résultante des forces sur l'échelle = 0 et limite de glissement et ...) , on a :

P = N (somme des forces verticales = 0)
R = f (somme des forces horizontales = 0)
f = µ.N (limite du glissement)

R.h - P.d = 0
µ.N.h - N.d = 0
d = µ.h
-----
On arrive, évidemment aux mêmes résultats par la méthode préconisée par picard.

merci bcp j-p

Bonjour J-P et bonjour Ahlambebe

bonj picard
ma faute est je crois a forces des appuis pas au moments et dans cette exo ils nya pas des appuis il ya une force de frottement