Inscription / Connexion Nouveau Sujet
Forces de pression sur un cylindre dans un fluide
Bonjour,
Nous travaillons en ce moment sur la Poussée d'Archimède. Pour cela on a étudié les forces de pression qu'exerce un fluide sur les différentes surfaces d'un cylindre. Le problème est que je ne comprends pas pourquoi sur un cylindre posé à la verticale les forces de pression sur la surface latérale sont nulles alors que si l'on prend un cylindre posé à l'horizontale ces mêmes forces ne sont pas nulles. Pourtant elles devraient s'annuler de la même façon non ?
Merci d'avance pour votre réponse.
bonjour,
je ne comprends pas pourquoi sur un cylindre posé à la verticale les forces de pression sur la surface latérale sont nulles
non, la RESULTANTE des forces de pression sur la surface latérale est nulle
revoir la démonstrAtion du théorème d'Archimède ici ->
les surfaces latérales subissent bien la pression du fluide, mais les forces se compensent
si le cylindre est couché, c'est pareil, la résultante des forces de pression est bien dirigée vers le haut
(cf dessin) et les efforts exercés sur les parois latérales (les disques à droite et à gauche) se compensent
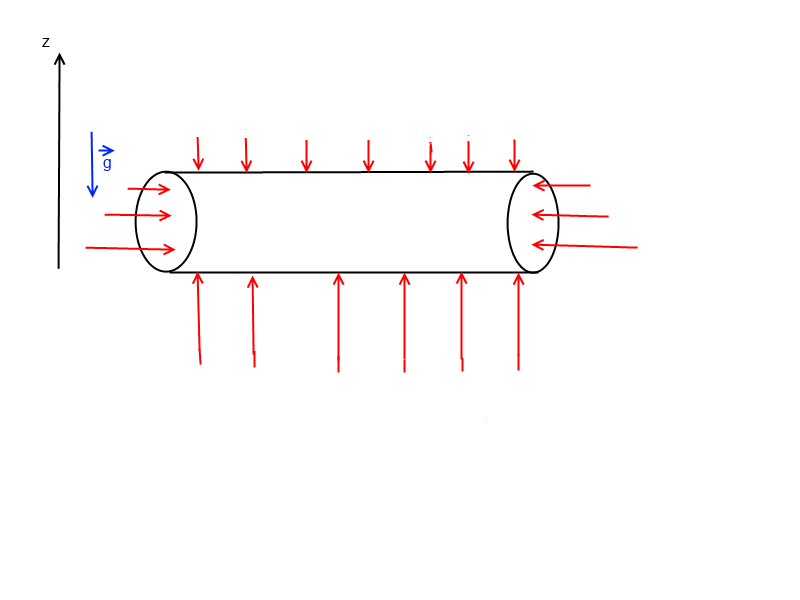
Ah oui d'accord je comprends mieux maintenant pour les forces latérales. Mais j'ai du mal à voir dans ce cas que la résultante des forces de pression est vers le haut vu qu'on a des forces dans le sens ez et dans le sens -ez. Pour moi ça s'annule aussi. Par le calcul effectivement on retrouve bien ce résultat mais de manière plus "visuelle" ce n'est pas évident.
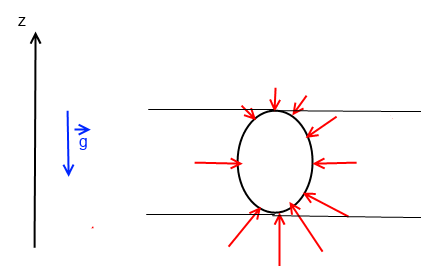
la pression augmente avec la profondeur (c'est pour cela que j'ai fait des flèches plus grandes en bas)
donc la résultante des forces de pression est non nulle selon (Oz)
si tu représentes une section du cylindre, tu vois que les forces sont plus importantes "en bas" qu'en haut
donc selon (Oz) la résultante est vers "le haut"
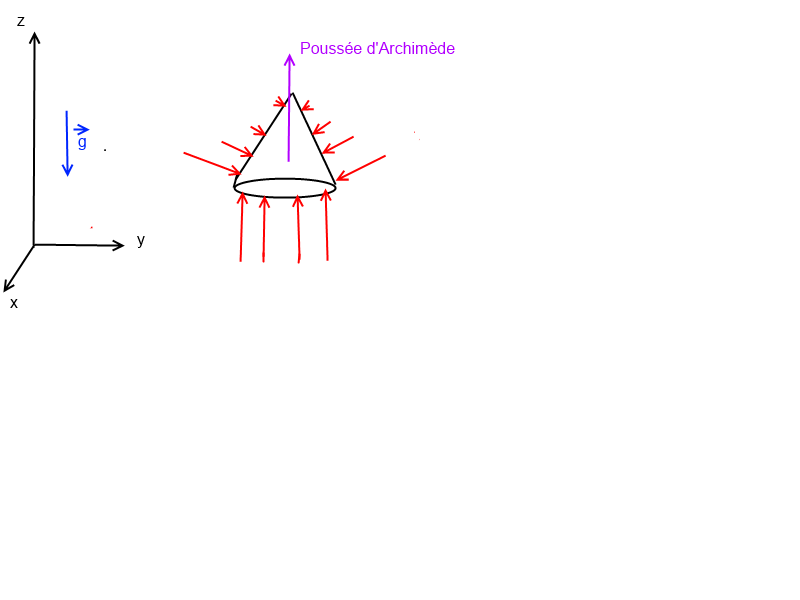
D'accord merci cela devient beaucoup plus clair dans ma tête. Une dernière question me travaille sur un cône a t-on la meme chose ? Je présume qu'on une force de pression sur la base du cône vers le "haut" et des forces latérales qui se compensent et donc s'annulent ?
le résultat est général et indépendant de la forme
pour un cône immergé on aurait ceci schématiquement:
les forces latérales ne se compensent qu'en projection sur (xOy), mais pas sur (Oz) !
la résultante est une force selon (Oz) donnée par le théorème d'Archimède, s'appliquant au cdm du volume de fluide déplacé