Inscription / Connexion Nouveau Sujet
Forces centrales (la suite)
Re bonsoir à tous !
C'est encore moi,toujours en maths sup, et bloquée sur un DM de physique avec plus de 70 questions...
J'ai vu qu'il ne fallait qu'un seul exercice par sujet alors je crée un nouveau sujet, pour la suite de mon DM, s'il ne fallait pas n'hésitez pas à me le dire et je ferais de mon mieux pour rectifier le tir.
L'exercice 3 s'intitule "Satellite Artificiel,Sonde spatiale".
L'énoncé de départ est le suivant :
" Un satellite articifiel S,assimilable à un point matériel de masse m, évolue librement, à grande distance de la Terre. La Terre est considérée comme un corps immobile, rigoureusement sphérique et homogène de rayon R, de masse M et de centre O. On désigne par vecteur r= vecteur OS le vecteur position du satellite et par vecteur v= d vecteur r/dt. A l'instant initial t=0, le satellite se trouve dans la position vecteur r0, animé de la vitesse vecteur vo, non radiale.
L'influence de la Lune, du Soleil et des autres planètes ainsi que celle de l'atmosphère sont ignorées. On étudie la situation pour t>0"
Je suis bloquée à différents endroits...
Dans la partie 2, qui se nomme "Etude du mouvement plan, aspects dynamiques et énergie", je suis bloquée à la question 4 qui est :
" On note respectivement U(r) et K(r) l'énergie potentielle et l'énergie cinétique du satellite dans la position courante r, et respectivement U0 et K0 ces mêmes énergies à l'instant initial.
Partant de la position vecteur r, le satellite effectue un déplacement élémentaires vecteur dr le long de sa trajectoire. Relier les variations dU(r) et dK(r) de l'énergie potentielle et cinétique observées au cours de ce déplacement."
D'après mon cours sur le sujet, on a Ec = -Ep/2 , démonstration simple en utilisant la vitesse constante d'un satellite en orbite géostationnaire. Or ici, nous n'avons pas cette information, la trajectoire n'est pas précisée (bien que dans la partie 1 nous ayons effectivement constaté que dans le cas général, elle était elliptique ou circulaire). J'ai tenté de dériver les énergies mais les résultats n'étaient pas liés, et je ne vois pas comment les relier...
Dans la partie 4, intitulée "Erreur de positionnement du satellite sur orbite":
"Selon les cas, des erreurs à la mise en position du satellite peuvent l'amener sur une trajectoire elliptique. L'équation polaire de la trajectoire du satellite dans le cas général s'exprime par r= p/ 1+ecos& (& représente un angle theta quelconque) (on suppose l'origine des angles polaires & convenablement choisie).
On montre que la valeur du paramètre p répond à p=C²/GM ou C est la constante des aires, G la constante universelle de gravitation et M la masse du centre attractif.
2) La mise en orbite du satellite est imparfaite. Il est placé à l'altitude h=a1-R (a1 est le rayon de l'orbite géostationnaire, j'ai trouvé a1=42150 km, R est le rayon terrestre), mais avec un vitesse de module v' légèrement grande que v1, de direction orthoradiale (j'ai trouvé précédemment v1= 3,08km/s, vitesse du satellite géostationnaire).
Représenter schématiquement la trajectoire obtenue. Quelles sont les nouvelles valeurs C',p' et e' prises par C,p et e ? (C,p,e dans le cas géostationnaire toujours,C=a1*oméga², ou oméga est la vitesse angulaire de rotation de la Terre,p=a1 et e=0)
Calculer numériquement les valeurs extrêmales rmin et rmax prise par la distance r entre le satellite et le centre de la Terre pour v'=3300 m/s
3) L'énergie mécanique E du satellite a une expression analogue à celle d'un satellite circulaire, en remplaçant dans cette expression le rayon par le demi grand axe a' de la trajectoire. En déduire la valeur de a' "
J'ai trouvé : C'=(a1-R)²*oméga, mais je ne suis déjà pas sûre de ça, car même pour la valeur de C j'ai vu certains mettre C=a1v1 (le résultat est très proche). La valeur de p' s'en déduit, ici pas de soucis.
En revanche pour la valeur de e'... Je n'ai absolument aucune idée de comment procéder, j'ai tenté de l'évaluer en utilisant l'équation polaire de la trajectoire, à l'apogée (ou au périgée) mais le résultat me semble étrange...
De même pour les valeurs de rmin et rmax, j'ai voulu utiliser l"équation avec les valeurs 0 et 180° mais cela me donne deux résultats inversés, soit un cercle et cela ne correspond pas, mais du coup je sèche...
Pour l'énergie mécanique, on a E= mv'²/2 - GMm/2a' soit a' = -GMm/(2E-mv'²) or on ne me donne pas la valeur de m, donc je ne vois pas comment déduire la valeur de a' de cette expression ^^
Et enfin, dans la 5ème partie nommée "Sonde Spatiale", il y a une première partie sur la première phase du mouvement de la sonde ,en orbite basse autour de la Terre, puis on a ceci:
" Le plan de vol prévoit une approche de Mars puis une poursuite du voyage en direction de Jupiter. La disposition des planètes impose alors de dévier la trajectoire de la sonde. Afin d'économiser tout moyen de propulsion, la sonde va utiliser le champ de gravitation martien pour cette opération. La suite de l'étude est dans le référentiel planéto-centrique Rm centré sur Mars.
Dans la première partie du mouvement, la sonde est suffisamment éloignée de Mars pour que l'on considère son mouvement comme rectiligne et uniforme, l'interaction de gravitation avec la planète étant infime. On note va la vitesse d'approche de la sonde dans ce référentiel. On note b la distance entre la droite support de la vitesse dans la phase d'approche et le centre de la planète, nommée paramètre d'impact.
1) Quelle sera la nature de la trajectoire suivie par la sonde à proximité de Mars ? Justifier.
2) Quelle est l'énergie Ea de la sonde dans le référentiel Rm ? Calculer la valeur Ca de la constante des aires pour la sonde. La trajectoire répond à l'équation polaire r= pa/1+eacos& (& un angle theta quelconque) avec pa=Ca²/GMa (Ma la masse de Mars)
Déterminer pa puis ea en fonction de b,va,G et Ma. On donne la relation entre l'énergie Ea du mobile,pa et ea: Ea=(GmMa)*(ea²-1)/pa
3) Etablir une condition sur b pour que la trajectoire de la sonde subisse en fin de processus une déviation de 10° par rapport à sa direction incidente.
4) A quelle altitude minimale ha la sonde va t-elle survoler la surface de Mars dans ces conditions ? On donne va=1.00x104m/s "
J'ai mis que la trajectoire serait elliptique, car le champ de gravitation martien est un champ newtonien.
J'ai ensuite trouvé Ea= mva²/2 - GmMa/Ra (Ra le rayon de Mars), mais là déjà je ne sais pas si l'énergie potentielle de gravitation doit être prise en compte, je ne sais pas si l'on se place loin ou proche de Mars ?
En considérant la première option, j'ai mis Ea = mva²/2, donc C=bva, pa=b²va²/GMa et grâce à la relation avec Ea et ea, j'ai trouvé ea= racine carrée de ((b²va4/2G²Ma² )+1)
Mon hypothèse est elle la bonne ou doit considérer également l'énergie potentielle de gravitation ?
Quant aux deux dernières questions, je me suis creusée la tête pendant 1h sans avoir d'idée à utiliser, je ne vois vraiment pas... J'ai pensé un instant à un angle &sortie qui devrait valoir &entrée +10, mais je ne vois pas comment m'en servir !
Voilà, désolé pour la longueur mais malgré déjà une semaine passée sur ce DM je bloqué désespérément à ces questions là, même si elles ne représentent qu'un dixième du reste cela m'énerve !
Merci à ceux qui prendront de leur temps pour m'aider, je vous en suis reconnaissante d'avance !
Miss
Bonjours, désoler de répondre pour dire sa, mais je suis fan de physique et j'aimerai bien avoir ton énoncé d'exercice pour tenté de le faire, peut tu me l'envoyer par mail ?
***Adresse courriel supprimée***
Merci beaucoup.
Bonjour
Un peu d'aide sur la partie 4, pour l'instant...
Par définition, la constante des aires est égale au quotient de la norme du moment cinétique du satellite par la masse de celui-ci. Dans le cas particulier où la vitesse est v'1, cela conduit à C'=a1.v'1 . Je ne comprends pas ton calcul : le moment cinétique se calcule toujours au centre O de l'astre attracteur. Selon la loi des aires, cette vitesse maximale correspond au périgée de la trajectoire : rmin=a1 .
Ensuite :
Pour apprécier le réalisme de ces résultats, il faut garder en tête que le cas particulier de la trajectoire circulaire correspond à : ... On "voit" bien ainsi ce qui se passe quand on remplace v1 par une valeur v'1 un peu supérieure.
Je n'ai pas terminé les calculs mais cela devrait tout de même t'aider...
Concernant la partie II, il est peut-être possible d'affirmer directement que la seule force appliquée : la force gravitationnelle, est conservative. L'énergie mécanique du satellite se conserve :
je fais tout de même la démonstration. La seule force appliquée est la force gravitationnelle :
J'exprime la travail élémentaire de cette force au cours d'un déplacement élémentaire de vecteur :
Ce travail élémentaire étant égal à une différentielle, on l'exprime comme l'opposé de la variation élémentaire d'énergie potentielle :
La constante est nulle puisque par convention, U tend vers zéro si r tend vers l'infini.
Le théorème de l'énergie cinétique appliqué au satellite au cours du déplacement élémentaire s'écrit :
Conclusion :
L'énergie mécanique E se conserve au cours du mouvement.
Remarque : il existe une démonstration plus rapide utilisant les propriétés du gradient...
Je n'avais pas pensé à utiliser cette définition de la constante des aires, effectivement je comprends un peu mieux, mais j'ai trouvé L=mr²v , du coup L/m me donnerait par exemple ici un a1²v'1 , ai-je fait une erreur dans le moment cinétique ?
Et oui effectivement on applique le moment cinétique par rapport au centre attracteur, je ne sais pas pourquoi j'ai pensé à changer ça alors qu'il ne faut pas ^^'
Autrement j'ai compris tout le reste, vos explications sont vraiment top, merci beaucoup ! Je manque encore cruellement de pratique pour penser à utiliser chaque égalité (même non citée dans l'énoncé) que je connais pour retrouver une inconnue.. Encore merci pour votre aide, elle m'est très précieuse !
Ah non après réflexion j'ai compris mon erreur, parce que theta point vaut aussi v1/a1 d'ou le carré qui disparait, ça me paraît tellement logique maintenant, pourquoi n'y ai je pas pensé avant !
Bonjour
J'ai mis que la trajectoire serait elliptique, car le champ de gravitation martien est un champ newtonien.
Les éléments de solutions fournis par le site que tu as référencé t'ont sans doute aidé car tes réponses sur cette partie sont fausses.
Le satellite provient de la terre, considérée comme infiniment éloignée de mars dans cette partie. Après passage à proximité de mars, le satellite s'en éloigne définitivement : en aucun cas la trajectoire ne peut être une ellipse !
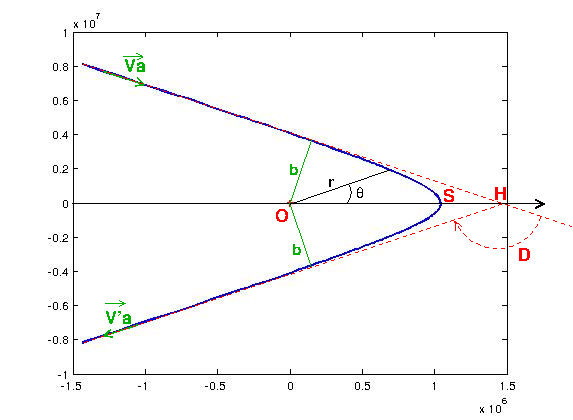
L'énergie potentielle loin de mars étant nulle alors que l'énergie cinétique vaut ½ mva2, l'énergie mécanique du satellite est positive et vaut ½ mva2 ; dans ce cas, la trajectoire est une branche d'hyperbole (voir démonstration dans ton cours). Loin de mars en venant de la terre, la trajectoire correspond à une asymptote de cette hyperbole dirigée par le vecteur vitesse va. Loin de mars en s'en éloignant, la trajectoire est l'autre asymptote ; la conservation de l'énergie conduit alors à un vecteur vitesse de même norme que va mais de direction différente, l'angle entre les deux direction étant la déviation D (voir figure). La conservation du moment cinétique conduit à l'égalité des distances du centre O de mars à chacune des asymptotes. Pour la suite, si les éléments de corrections indiqués sur le site ne sont pas suffisants, demande de l'aide !
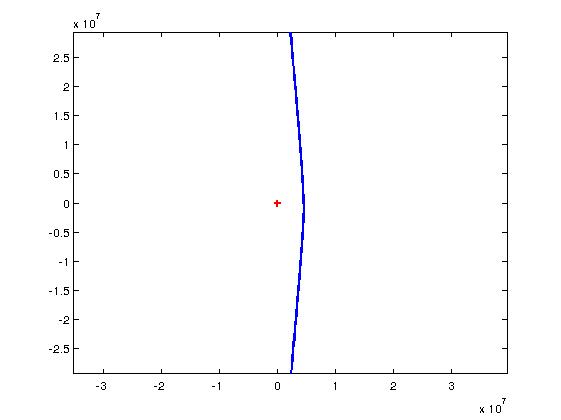
Voici un tracé de la trajectoire (croix rouge : centre de mars) : en repère orthonormé, la faible valeur de D (10°) rend ce schéma peu explicite. Sur le second schéma, l'axe des abscisses est dilaté d'un facteur voisin de 10 : la visibilité est bien meilleure mais attention aux déformations ainsi engendrées : l'angle D est très fortement augmenté ; d'autre part, la distance minimale au centre O est obtenue réellement au point S, ce qui n'apparaît pas sur la figure compte tenu de la forte dilatation des distances horizontales...
Bonjour,
encore merci pour toutes ces explications ! j'ai compris le principe (ce qui n'était déjà pas gagné) pour le calcul de b, mais même avec la conservation du moment cinétique, je ne vois pas comment l'écrire... En écrivant l'égalité des moments cinétiques on peut effectivement faire apparaître l'angle de déviation, mais du coup comme b est le même, je ne vois pas comment le calculer à partir de ça ! A moins que la réponse ne soit simplement le fait que b est le même en approche ou en départ ?
Et du coup l'altitude Ha correspond à la distance OS , mais même en ayant la valeur de b je ne vois pas comment la calculer, faut-il utiliser l'équation de la trajectoire ?
Bonsoir
La conservation du moment cinétique permet seulement de prouver que les deux asymptotes sont toutes deux distantes de b du centre O de Mars. Une fois déterminée l'équation de l'hyperbole, les directions des deux asymptotes correspondent à r
 soit à cos(
soit à cos( )=-1/e
)=-1/e
Cela va te donner les deux valeurs de  possibles et tu en déduiras la valeur de D. Le schéma ci-dessus devrait t'aider...
possibles et tu en déduiras la valeur de D. Le schéma ci-dessus devrait t'aider...
Bonjour
Quelques indications supplémentaires qui devraient te permettre de terminer seule ce problème.
Loin de mars et de la terre, l'énergie potentielle est nulle. La conservation de l'énergie mécanique impose donc l'égalité des deux énergies cinétiques :
Moment cinétique en O, loin de mars avant l'approche de mars :
D'où la constante des aires :
Ce résultat est cohérent avec l'expression générale de la constante des aires : car ici :
. En inversant le sens de circulation le long de la trajectoire sans changer les sens d'orientation de
et de
, on obtiendrait
...
Loin de mars après passage au voisinage de cette planète, le moment cinétique en O a pour expression :
La conservation du moment cinétique conduit à :
L'énergie mécanique étant positive, la trajectoire est une branche d'hyperbole (voir le cours). Cela est cohérent avec la formule de l'énergie fournie : une énergie mécanique positive correspond nécessairement à une excentricité de la conique strictement supérieure à 1.
Les asymptotes correspondent à : soit à :
. Les deux valeurs possible de
sont, exprimées en degrés :
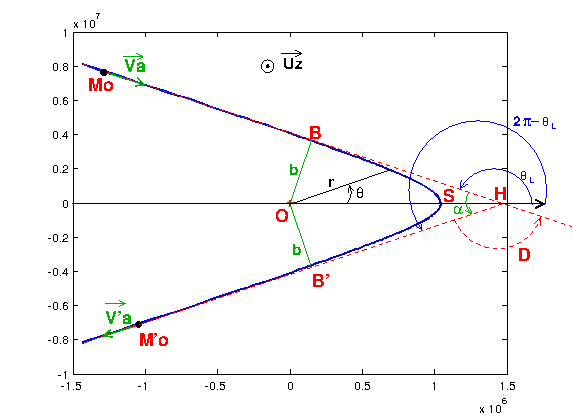
En observant le schéma, on remarque :
Soit :
La suite est facile : la formule fournie pour l'énergie permet d'obtenir la valeur du paramètre de l'hyperbole :
Ayant ainsi la valeur du paramètre, la relation avec la constante des aires permet d'obtenir b :
La valeur minimale de la distance du satellite à mars est obtenue pour une valeur maximale de soit pour
, ce qui correspond au point S de la trajectoire :
Y'a juste un truc que je n'ai pas compris dans vos réponses ce que vous faites du h=a1-R dans la partie 4 ..


 profil
profil à côté de votre pseudo). De plus, l'affichage de cet email est même géré de façon à gêner sa récupération par d'éventuels robots spammeurs, sans pour autant gêner l'affichage pour les membres réels du site.
à côté de votre pseudo). De plus, l'affichage de cet email est même géré de façon à gêner sa récupération par d'éventuels robots spammeurs, sans pour autant gêner l'affichage pour les membres réels du site.

