Bonjour
Il faut commencer par déterminer l'expression du vecteur champ créé par l'anneau chargé en tout point de l'axe (Ox). Commencer par raisonner sur les symétries pour obtenir la direction du vecteur champ puis appliquer la loi de Coulomb.

Tu te contentes de fournir l'expression du vecteur champ créé par une charge ponctuelle q. Il s'agit ici de déterminer le vecteur champ créé par l'anneau chargé en un point M quelconque de l'axe (Ox). Ensuite, tu pourras considérer que la force exercée par l'anneau chargé sur la charge ponctuelle situé en M est :



Avant tout calcul, il faut faire l'inventaire des éventuels plans de symétyrie ou d'antisymétrie de la source du champ contenant le point M. Cela doit être dans ton cours. Sinon : tu trouveras cela aux paragraphes I et II du document ci-dessous :

PS : la partie VII du document, inutile ici, pourra t'être utile si tu dois appliquer le théorème de Gauss...

Inventaire des éventuels plans de symétrie ou d'antisymétrie :

*On a un plan de symétrie si les densités de charge des deux points P et P' du plan de l'anneau sont positifs.



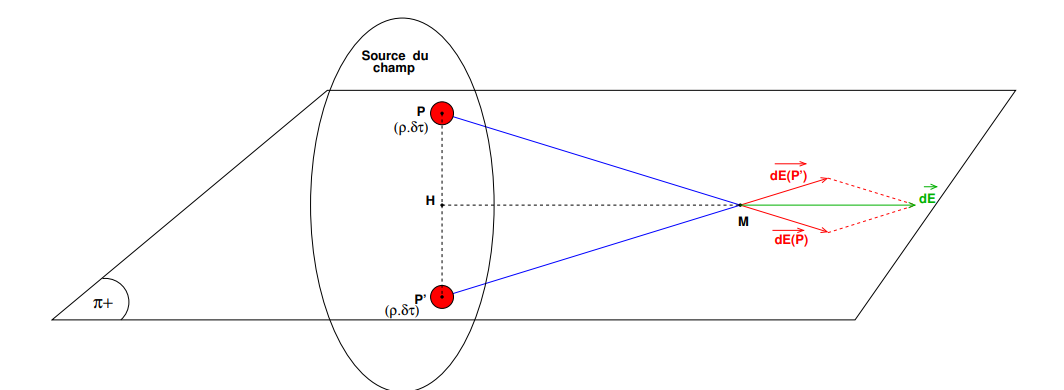
Alors avec ( R étant le rayon de l'anneau).

* On a un plan d'antisymétrie si les densités de charge des deux points P et P' du plan de l'anneau ne sont pas tous les deux positifs c'est à dire l'une positive et l'autre négative.



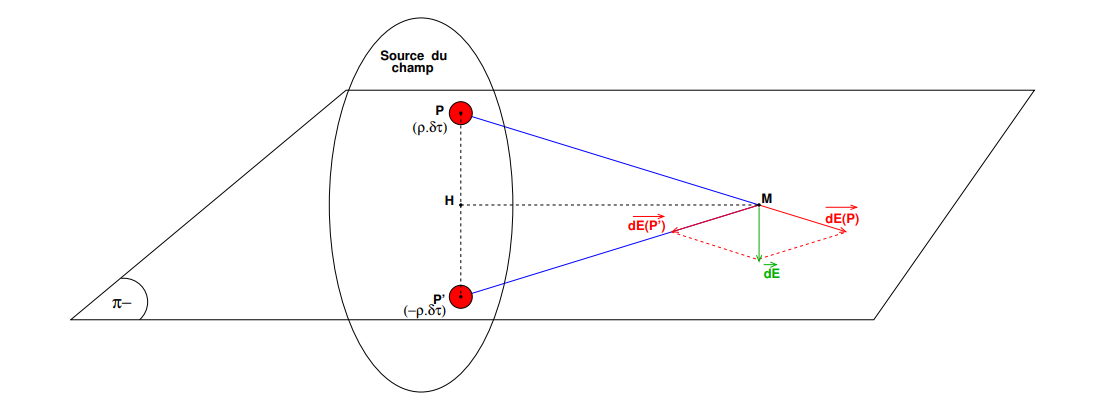
Alors avec ( R étant le rayon de l'anneau).

La source du champ est ici une distribution lineique de charge en forme d'anneau. Que vient faire ici une formule correspondant au vecteur champ électrique créé par une charge ponctuelle  ?

Ah oui donc   avec ( R étant le rayon de l'anneau) et

Et   ( R étant le rayon de l'anneau) et

D'où vient cette formule, qui de plus est fausse ?
De toutes les façons, j'imagine que tu dois fournir une démonstration. Reprends mon message du  05-11-21 à 14:49.

Inventaire des éventuels plans de symétrie ou d'antisymétrie :

*On a un plan de symétrie si les densités de charge des deux points P et P' du plan de l'anneau sont positifs.



Alors est horizontal et perpendiculaire au plan de l'anneau.

* On a un plan d'antisymétrie si les densités de charge des deux points P et P' du plan de l'anneau ne sont pas tous les deux positifs c'est à dire l'une positive et l'autre négative.



Alors est vertical et parallèle au plan de l'anneau.

Comment trouver ces expressions ?

Le raisonnement est plutôt bien détaillé ici :

OK mais est ce que je dois remplacer la charge q par la densité linéique ?

Il s'agit d'étudier le vecteur champ créé par la charge Q répartie sur le cerceau. La densité linéique de charge du cerceau est donc :


Je me répète :
Il s'agit ici de déterminer le vecteur champ \vec E créé par l'anneau chargé en un point M quelconque de l'axe (Ox). Ensuite, tu pourras considérer que la force exercée par l'anneau portant la charge Q sur la charge ponctuelle q située  en M est :

\vec F=q\cdot\vec E

J'ai oublié d'activer les balises "tes" pour la dernière formule...

Il s'agit d'étudier le vecteur champ créé par la charge Q répartie sur le cerceau. La densité linéique de charge du cerceau est donc :


Je me répète :
Il s'agit ici de déterminer le vecteur champ \vec E créé par l'anneau chargé en un point M quelconque de l'axe (Ox). Ensuite, tu pourras considérer que la force exercée par l'anneau portant la charge Q sur la charge ponctuelle q située  en M est :

Ok, donc

En effet ; ; ici car la charge Q parcourt l'anneau de surface

L'énoncé définit la variable Q mais pas la variable . On peut utiliser dans les calculs intermédiaires mais le résultat final doit faire intervenir Q et non .

D'accord ;

merci beaucoup