Inscription / Connexion Nouveau Sujet
Force de rappel d'un ressort... Plutôt tordue
Bonsoir !
J'essaie de faire un exercice de mécanique, et pour celui-ci je dois trouver (entre autres) l'expression de la force de rappel d'un ressort, et j'avoue que je suis plutôt perdu.
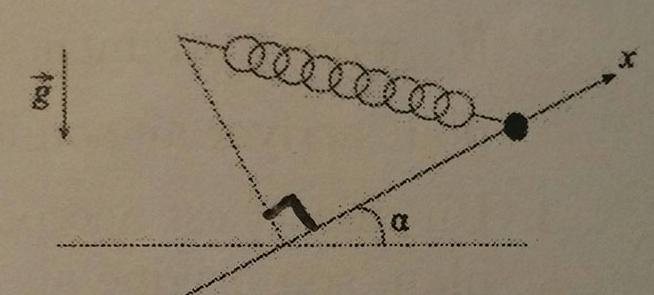
En gros, on a un point M qui peut se balader sur Ox, Ox étant incliné d'un angle par rapport à l'horizontale. On accroche à une distance D (au point A) de l'axe un ressort de longueur à vide D au point M. L'origine des x est le point O, projeté orthogonal de A sur Ox. On suppose x << D
Je dois, comme je l'ai dit, trouver la force de rappel du ressort. On appelle l'angle (OA, OM) . Après calculs simples et en utilisant l'hypothèse, on trouve que
.
Ensuite, la force de rappel :
Ma difficulté est pour trouver la longueur l, je ne vois pas comment le faire... C'est compliqué en utilisant les relations trigonométriques étant donné qu'on ne peut pas composer les équivalants...
Comment trouver cette longueur ?
Merci d'avance,
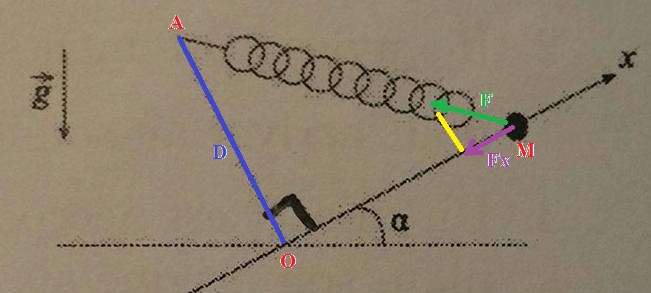
Pythagore dans le triangle AOM :
AM² = AO² + OM² (1)
Avec L la longueur du ressort, on a : AM =L
Soit x l'abscisse de M ---> OM = x
(1) --->
L² = D² + x²
L = V(D²+x²) (avec V pour racine carrée)
F = -k.(L - Lo)
F = -k.(V(D²+x²) - Lo)
-----
Si on veut uniquement la composante de F suivant Ox, alors :
Fx = F * cos(OMA)
OM = AM.cos(OMA)
x = V(D²+x²) * cos(OMA)
Fx = -k.(V(D²+x²) - Lo) * x/V(D²+x²)
-----
Sauf distraction. 


