Inscription / Connexion Nouveau Sujet
Force de Laplace
Bonjour,
Pourriez-vous m'aider sur l'exercice suivant :
On considère une particule chargée dans un champ électromagnétique soumise à la force de Lorentz. On se place dans le cas d'un champ magnétique uniforme () et d'un champ élec nul. A l'instant initial, on a
et
.
On demande :
1) Pour une charge , résoudre l'équation pour la vitesse :
avec
2) Donner les équations horaires du mouvement
3) Montrer que la projection du mouvement dans le plan xOy est uniforme et décrit un cercle.
Mes tentatives de réponse :
1) avec
Donc après intégration et application des conditions initiales on a :
(Je ne vois pas où intervient le fait que . J'ai dû rater quelque chose.
2) On intègre :
3) Pour montrer que c'est un cercle, il faut que je montre que . Ca n'a pas l'air de fonctionner pour moi.
Merci pour votre aide !
La situation est nettement plus compliquée !
Ton énoncé n précise pas ce qu'il appelle v dans l'expression :
Sinon : la relation fondamentale de la dynamique doit être projeter sur les trois axes.
Cela conduit bien à v3=constante. En revanche : Pour les deux autres 
n obtient :
dv1/dt : fonction de 
et de v2
dv2/dt : fonction de et de v1.
L'intégration n'est donc pas évidente...
Le signe de influence le sens du mouvement le long de la trajectoire.
Commence par écrire proprement les équations différentielles. Je t'aiderai ensuite si tu n'arrives pas à obtenir les expressions de v1 et de v2 en fonction de t et des paramètres du problème.
Merci pour votre aide.
Dans l'énoncé, on me dit que est la vitesse de la particule, rien de plus.
Je ne vois pas comment obtenir en fonction de
et
:
Le produit vectoriel me donne :
.
Puis :
Sur :
Sur :
Sur :
d'où les équations différentielles couplées :
On en déduit : v3= constante ; z=v3.t : mouvement rectiligne uniforme suivant z.
Reste à montrer que le mouvement du projeté de la particule dans le plan (Oxy) est un mouvement circulaire uniforme de vitesse angulaire .
Pour résoudre le système formé des deux premières équations différentielles, on peut dériver la première équation puis procéder par substitution en tenant compte de la seconde. Tu obtiens une relation très simple entre v1 et sa dérivée seconde par rapport à t. Méthode analogue pour v2.
La relation concernant la date t= O : n'apporte aucune information particulière. Elle est équivalente à :
expression de la norme du vecteur vitesse initiale puisque à t=0 : v2=0. Il y a tout de même un problème d'énoncé car v1,v2,v3 désignent les coordonnées du vecteur vitesse à la date t. Il serait donc préférable de noter v01 et v03 les valeurs particulières de v1 et de v3 à la date t=0.
J'obtiens :
Ce qui donne :
Donc :
ou
Puis
Pour les conditions initiales, je ne vois pas comment faire puisque j'ai 4 constantes...
Les racines de l'équation caractéristique sont 
i. et non . Les solutions sont donc sinusoïdales de la forme :
v1 = A.cos(.t)+B.sin(.t)
v2 = C.cos(.t)+D.sin(.t)
Les constantes A, B, C et D sont à déterminer en fonction des conditions initiales. Elles vont faire intervenir v01 et v02 .
Merci !
A t=0, je vais pouvoir déterminer A et C mais pour B et D je ne vois pas comment faire puisque .
De plus, les conditions initiales me donnent 2 équations et j'ai 4 inconnues.
x(t)=[-A.sin(.t)+B.cos(.t)]
y(t)=[-C.sin(.t)+D.cos(.t)]
La connaissance des vitesses initiales et des coordonnées initiales fournit quatre équations pour quatre inconnues.
PS : j'aurais dû te le faire remarquer dès mon premier message : la force exercée sur une particule chargée placée dans un champ électromagnétique est la force de Lorentz. La force de Laplace est la force magnétique exercée sur un conducteur parcouru par un courant et placé dans un champ magnétique.
Grossière erreur dans mon message précédent : en dérivant par rapport au temps l'expression de la vitesse, on obtient l'accélération. Il faut donc écrire :
ax(t)=[-A.sin(.t)+B.cos(.t)]
ay(t)=[-C.sin(.t)+D.cos(.t)]
en reprenant les relations de mon message du 21-01-22 à 16:37 dans le cas particulier des conditions initiales :
ax(0) =-.v02
ay(0) =.v01
Tu as là les deux relations manquantes pour obtenir les quatres constantes A, B, C et D.
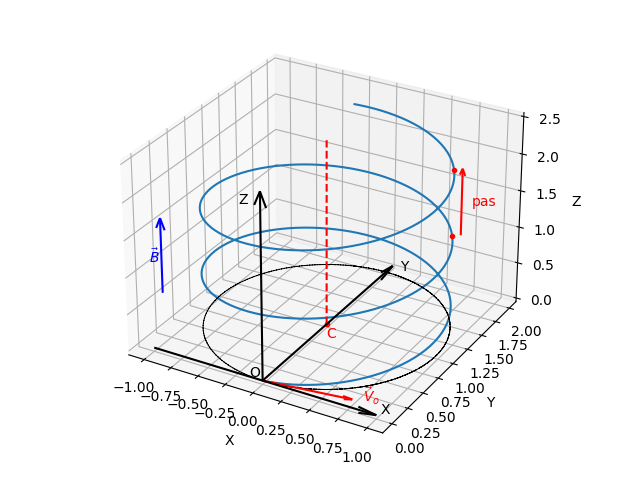
C'est bien cela ! Le mouvement en 3D est la composition d'une translation suivant (Oz) à la vitesse constante v03 et d'une rotation à vitesse angulaire constante autour de l'axe (C,z). (voir allure de la trajectoire ci-dessous ; hélice tracée avec une échelle totalement arbitraire).
Remarque : en cas de particule de charge positive, la particule aurait été déviée à la date t= 0 dans le sens des y<0.Le point C aurait eu pour coordonnées (0, -R, 0) avec :
Annuler
connectez vous