Inscription / Connexion Nouveau Sujet
Focométrie de lentilles minces convergentes
Bonjour,
J'ai un petit exercice d'optique qui me pose quelques problèmes. Je vous donne l'énoncé :
"On se propose de déterminer expérimentalement la vergence C=1/f' d'une lentille mince convergente L, de centre optique O, de distance focale f' inconnue, placée dans l'air.
La lentille donne d'un objet AB une image A'B' nette sur un écran E (AB et E sont perpendiculaires à l'axe optique de L)."
1) Lorsque le point objet A (OA=p) se déplace sur l'axe :
a) comment varie la distance objet-image D=AA' en fonction de la distance p ?
b) comment varie le gradissement linéaire 
=\overline{A'B'}/\overline{AB} ?
c) tracer les graphes D(p) et (p) dans les intervalles physiquement acceptables.
---------------------------------------------------------------
J'ai trouvé =(p+D)/p.
Je suis bloqué car je ne trouve pas comment exprimer D en fonction de p, donc je ne peut pas tracer les graphes de (p) et D(p)..
Si vous pouviez m'aider, ça serait gentil ^^.
Oups il semblerait que j'ai loupé mon coup, la question b) est la suiante :
b) comment varie le grandissement linéaire = valeur absolue de (A'B') / valeur absolue de (AB)
Bonjour,
Pour ma part, je ne sais pas faire d'optique géométrique autrement qu'avec des axes orientés et des distances algébriques. Pour maintenant il me semble trop tard pour que je change...
Formule de conjugaison pour une lentille mince de centre O, formule dite de Descartes
Le pied de l'objet est en A
Le pied de l'image est en A'
Le foyer image est en F'
L'axe optique est orienté (dans le sens de propagation de la lumière)
Puisque l'image est recueillie sur un écran, la position de l'objet définie par n'est pas quelconque...
La distance (positive) entre l'objet et l'image (l'écran) vaut
On trouve facilement que :
D'où le graphique suivant :
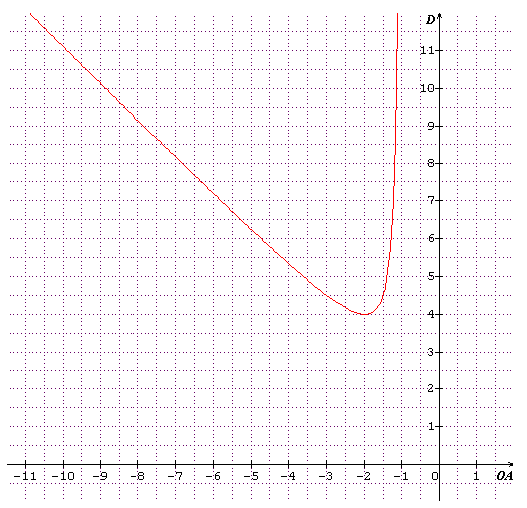
Pour l'axe des abscisses, la variable est et l'unité est f' =
Annuler
connectez vous