Inscription / Connexion Nouveau Sujet
Flux thermique à travers une double paroi
Bonjour à tous ! Je suis bloqué dans cet exercice qui pourrait bien tomber à mes examens de fin d'année, j'aimerais donc que vous m'aidiez à m'en sortir svp  Je bloque à partir de la 7.
Je bloque à partir de la 7.
Enoncé :
Soit une double paroi constituée de deux parois simples P1 et P2 telles que :
Paroi P1 :
- Facteur de conductivité thermique : K1 = 0.04 W m-1 K-1
- Epaisseur : L1 = 1 mm
- Surface : S1 = 200 cm²
Paroi P2 :
- Facteur de conductivité thermique : K2 = 0.10 W m-1 K-1
- Epaisseur : L2 = 2 mm
- Surface : S2 = 200 cm²
Cette double paroi sépare deux zones de température θ1 = 95 °C et θ2 = 32 °C. On fera l'hypothèse que, dans ces deux zones, il n'y a pas de phénomène de convection et que, par conséquent, ces températures θ1 et θ2 restent constantes au cours du temps. De plus, la température à l'interface P1 - P2 est supposée constante.
1. Dire pourquoi pouvons nous travailler en régime stationnaire ?
2. Par analogie avec l'expression de la résistance électrique R démontrée en TP et que l'on rappellera ici, donner l'expression de la résistance thermique RT d'une paroi simple d'épaisseur L et de facteur de conductivité thermique K.
Note : On exprimera la résistance électrique en fonction de la conductivité électrique, de
la longueur L de parcours des charges et de la surface S traversée par ces charges.
3. Rappeler l'expression de la loi d'Ohm en courant continu pour une résistance électrique R.
4. Donner l'expression de la résistance équivalente REq. calculée dans le cas d'un montage Série de deux résistances électriques de valeurs R et R'.
5. Les deux parois de facteurs de conductivité thermique K1 et K2 sont en contact en mode Série. Donner l'expression de ΔT = T1 - T2 en fonction de la résistance thermique équivalente RT Eq..
6. Calculer, en régime stationnaire, le flux de chaleur Φ après avoir expliqué pourquoi Φ(x) = Φ = Cte.
7. Déduire du résultat de la question précédente, la valeur de la densité de flux thermique jQ.
8. Après avoir rappelé l'expression de la loi de Fourier, on établira la dépendance en x de la température au sein de la paroi P1. Par simple analogie, exprimez la dépendance en x de la température au sein de la paroi P2.
9. En partant de l'expression de la résistance électrique R utilisée à la question 2., donnez l'expression de la résistance équivalente REq. calculée dans le cas d'un montage Série de deux résistances électriques caractérisées par (L1 et σ1, d'une part, et L2 et σ2, d'autre part).
10. En déduire, par analogie, la résistance thermique équivalente RT Eq.sachant que la longueur traversée « équivalente » est LEq. = L1 + L2 et que la section traversée S est la même en tout point.
11. Calculez, à partir de l'expression ci-dessus, la valeur du facteur de conductivité thermique équivalent KEq.
Mes réponses :
1) Les températures sont constantes, donc indépendantes du temps: le régime est stationnaire
2) R = (1/ )(L/S)
)(L/S)  RT = (1/K)(L/S)
RT = (1/K)(L/S)
3) U = RI
4) Montage en série donc Réq =  Ri = R + R'
Ri = R + R'
5)  T = T1 - T2 = Φ
T = T1 - T2 = Φ Li/(KiSi) = ΦRTéq
Li/(KiSi) = ΦRTéq
6)  T = cte, RTéq = cte, donc Φ = cte
T = cte, RTéq = cte, donc Φ = cte
Φ =  T/RTéq = ((95+273)-(32+273))/(0.001/(0.04*0.02)+0.002/(0.10*0.02)) = 28 W
T/RTéq = ((95+273)-(32+273))/(0.001/(0.04*0.02)+0.002/(0.10*0.02)) = 28 W
7) jQ = Φ/S = 28/0.02 = 1400 W/m²
Mes problèmes commencent là ! La prof m'a dit cette démarche pour la 7) mais pourquoi on n'additionne pas les surfaces, puisqu'il y a deux plaques  :? Je n'arrive pas non plus à la suite.
:? Je n'arrive pas non plus à la suite.
Merci d'avoir lu le sujet ! En espérant avoir des réponses à mes maux 
bonjour
loi de Fourier:  = -K
= -K T
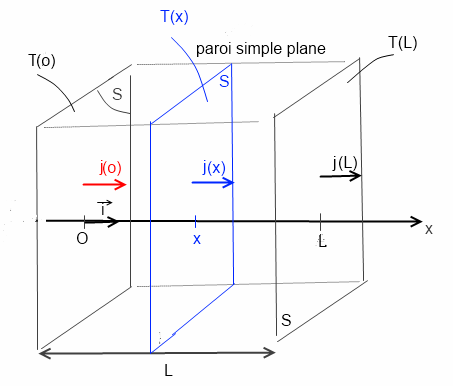
dans le cas d'une paroi plane de largeur L de surface S et de conductibilité K (cf dessin)
en régime permanent: T = T(x)
 = -K
= -K T = -K
 T/
T/ x
x 
donc j = j(x) = -K dT/dx
comme  = jS = cste
= jS = cste
on en déduit: dT = - /(KS) dx avec -
/(KS) dx avec - /(KS) = cste
/(KS) = cste
càd  T = -
T = - /(KS)
/(KS)  x
x
donc T est une fonction affine de x