Niveau licence

flux et circulation

Posté par
azerty4 30-01-19 à 22:10

Bonsoir,

j'ai quelques soucis pour prouver le théorème d'Ostogradski :

On a $\vec V = \alpha y² \vec x + \beta z² \vec y + \gamma x² \vec z$

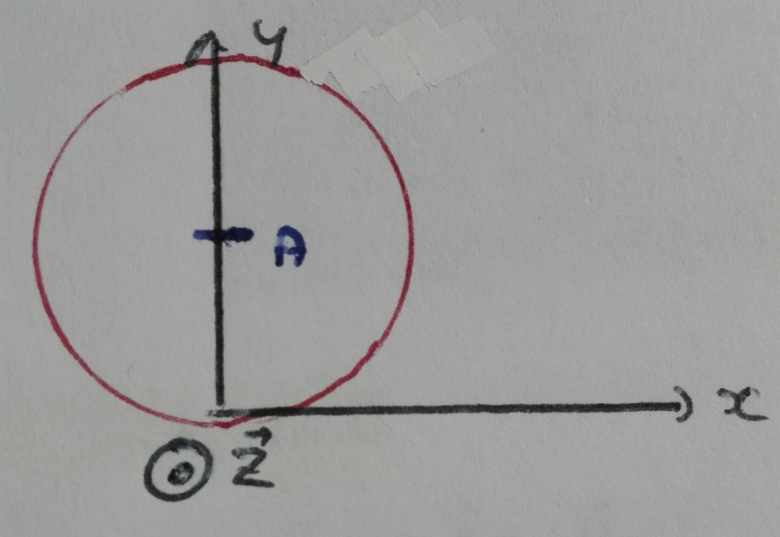
• On souhaite calculer le flux de rot(V) à travers la surface S (cercle de centre (0,a) et de rayon a)

J'ai utilisé les coordonnées polaires et j'ai avec x = rcos() et y = a+r sin() $d\phi = ... * 0 + ... * 0 + ( -2y \alpha dS)$

En intégrant $\phi = \int_{0}^{2\pi}{\int_{0}^{a}{(-2\alpha (a+rsin\theta) ) r dr d \theta }} = -\frac{2}{3}a^3 \alpha + 0$

• On souhaite calculer la circulation de V le long du contour du cercle, et arriver au même résultat

Je ne vois pas vraiment comment y arriver (ni même si la première question est bonne), avez vous des pistes ?

Merci d'avance pour votre aide

Bonne soirée

Posté par re : flux et circulation 30-01-19 à 22:11

(voilà le représentation de la surface)

flux et circulation

Posté par re : flux et circulation 30-01-19 à 23:26

Bonsoir
Je crois qu'il faut que tu revois sérieusement ton cours. Le théorème d'Ostrogradski concerne le flux d'un vecteur champ à travers une surface fermée ; il peut se calculer à partir de la divergence de ce vecteur vecteur.
À mon avis ici, il s'agit de vérifier sur un exemple le théorème de Stokes : la circulation d'un vecteur champ le long d'un contour fermé peut se calculer comme le flux du rotationnel de ce vecteur à travers une surface délimitée par ce contour pour peu que sens de la circulation et sens positif du vecteur surface soient choisis de façon cohérente..
Ensuite, peux-tu détailler ton calcul intégral ? les variables r et ne sont pas indépendantes...
Pour la circulation : tu peux raisonner en coordonnées cartésiennes en posant le vecteur déplacement élémentaire sous la forme :
$\overrightarrow{dl}=dx.\overrightarrow{x}+dy.\overrightarrow{y}+dz.\overrightarrow{z}$
Cela te permet ensuite d'exprimer simplement la circulation élémentaire $dC=\overrightarrow{V}.\overrightarrow{dl}$ sachant que le déplacement s'effectue le long du cercle donc à z=constante=0.

Posté par re : flux et circulation 31-01-19 à 00:02

Bonsoir,

C'est bien au théorème de Stokes qui lie les intégrales simples et doubles de $\vec A \vec dl$ et $\vec rot {(\vec A)} \vec {dS}$ auquel je pensais j'inverse souvent les 2 noms désolé :/

Pour le flux, j'avais pensé que dS orienté suivant z, donc seule la composante $-2y \alpha$ du rotationnel de $\vec V$ (celle suivant z) qui est utile, les autres s'annuleront avec le produit scalaire

pour le détail de l'intégrale l'intégrale j'avais $\phi = -2 \alpha \int_{r=0}^{a}{\int_{\theta=0}^{2 \pi }{(a+r sin \theta )} } r dr d\theta$ (j'ai posé en coordonnées polaires $dS = r dr d\theta$

$\phi = -2 a \alpha * 2 \pi \int_{r=0}^{a}{rdr} - 2 a \alpha \int_{0}^{2\pi }{sin\theta } \int_{0}^{a}{r²} = \frac{-2a²}{3}\alpha -0$

est ce correct ?

Merci pour votre aide

Bonne soirée

Posté par re : flux et circulation 31-01-19 à 00:06

(j'ai oublié le 2 pour le résultat final : $\phi = - \alpha \frac{2a²}{3} * 2\pi$ ce qui colle plus pour les dimensions, mais je pense commettre des erreurs de raisonnement)

Posté par re : flux et circulation 31-01-19 à 11:59

Maintenant que tu as précisé l'orientation de ton vecteur surface, je peux dire que je suis d'accord avec ton expression du flux :

$\phi=-2\alpha\cdot\iint_{disque}y\cdot dS$

Une analyse dimensionnelle élémentaire montre que l'expression du flux est de la forme :

$\phi=-\alpha\cdot K\cdot a^{3}$

où K est une constante positive sans dimension (de dimension 1 comme on dit plutôt). Je reprends ton calcul en séparant les variables :

$\phi=-2\alpha\cdot\left[a\cdot\int_{0}^{a}r.dr\cdot\int_{0}^{2\pi}d\theta-\int_{0}^{a}r^{2}.dr\cdot\int_{0}^{2\pi}\sin\left(\theta\right).d\theta\right]$

Le second terme est nul, donc :

$\phi=-2\alpha\cdot a\cdot\frac{a^{2}}{2}\cdot2\pi=-2\pi.\alpha.a^{3}$

Je te laisse calculer la circulation. Attention au sens positif de circulation !

Posté par re : flux et circulation 31-01-19 à 14:33

Merci pour votre aide c'est beaucoup plus clair

Pour la circulation, en choisissant le sens positif lié à l'orientation de dS avec la main droite, j'ai $\zeta = \alpha y² dx + \b[tex]\zeta = \oint_{0}^{2\pi }{\alpha (a²+2a* sin(\theta ) + a²sin²(\theta ) })* - a sin(\theta )$
eta z² dy + \gamma x² * 0[/tex] comme z = 0, seule la première partie est utilie et avec $y = a + a sin(\theta )$ et $dx = - a sin (\theta )$ on retrouve $\zeta = \oint_{0}^{2\pi }{\alpha (a²+2a* sin(\theta ) + a²sin²(\theta ) })* - a sin(\theta ) d \theta$
Avec les termes qui s'annulent, on retrouve bien $\zeta = \oint_{0}^{2\pi }{\alpha (2a* sin(\theta )}* - a sin(\theta ) d \theta = -2 \pi \alpha a^3$

Ce qui vérifie bien le théorème de Stokes !

Merci beaucoup pour votre aide !!

Bonne journée

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

flux et circulation

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique