Bonsoir j'ai un exercice sur l'application du théorème d ampère mais j'arrive pas à faire les deux dernières questions merci de bien vouloir m'aider

Énoncé

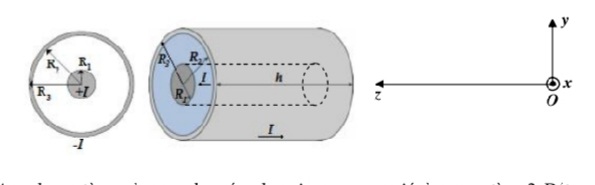
Un câble coaxial est constitué d'un conducteur cylindrique central de rayon R1 parcouru par un
courant d'intensité I (orienté suivant Oz). Le retour du courant de même intensité I se fait par un
conducteur cylindrique creux de rayon intérieur R2 et de rayon extérieur R3 (voir figure ci-dessous).
La densité volumique de courant est uniforme dans les conducteurs et la longueur est bien
supérieure aux rayons des cylindres considérés infinis, (R3 > R2 > R1)
1)
Préciser le système de coordonnées le mieux approprié à ce système? Déterminer la
direction du champ magnétique.

On choisit les coordonnées cylindriques parcequ'on on a une symétrie cylindrique
Tout plan perpendiculaire à (oz) est un plan d'antisymetrie ==>> le champ est suivant e(teta)

Determiner les variables dont dépend le champ magnétique

Le champ dépend de r parcequ'il y a invariance par translation suivant Oz et par rotation d angle teta

A l'aide du théorème d'Ampère, donner l'expression du module du champ magnétique crée
en tout point M situé à l'intérieur du conducteur central en fonction de 0, I, R1 et r (dessiner sur le
schéma ci-dessous le contour utilisé)

B= (Uo I r) / (2piR1²)

A l'aide du théorème d'Ampère, donner l'expression du module du champ magnétique crée
en tout point M situé dans l'espace entre les deux conducteurs en fonction de 0, I et r (dessiner sur
le schéma ci-dessous le contour utilisé)

B= (Uo I ) / (2pi r )

Déduire des calculs précédents, l'expression du flux
du champ magnétique crée entre
les deux conducteurs pour une longueur    l  du câble coaxial

D'après ce j ai compris dans cette partie le câble coaxial ne sera plus infini je vois pas pourquoi on doit déduire des autres résultats alors