Flux du champ magnétique : exercice de sciences physiques de école ingénieur

 Niveau école ingénieurPartager :
			        
					
				
Flux du champ magnétique 
Posté par 
MEV  31-12-20 à 11:26
Bonjour , SVP besoin d'indications pour résoudre cet exercice . 

 Exercice

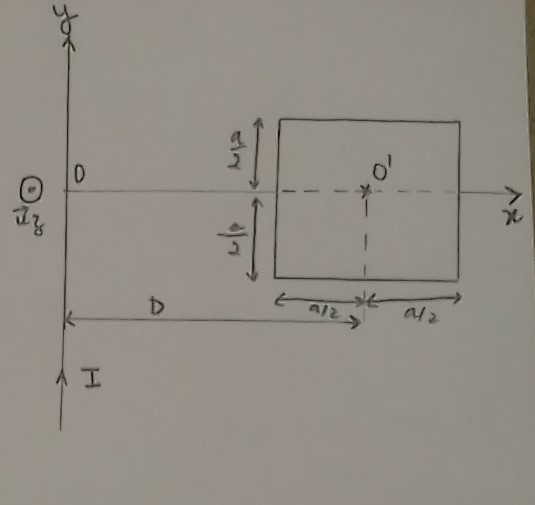
Evaluuer le flux magnétique envoyé par le fil rectiligne infini ( de direction Oy ) parcouru par le courant d'intensité I à travers le contour carré ( de coté a ) situé dans le plan Oxy et de normale orientée suivant z , tel que OO'=D ( O' centre du carré ) et D>   . 

Merci d'avance . 
 Posté par 
MEVre : Flux du champ magnétique   31-12-20 à 11:35
La définition du flux magnétique est : 

=
 Posté par 
MEVre : Flux du champ magnétique   31-12-20 à 11:44
Pour ce carré ,  

et B= (0.I)/2r suivant 
 Posté par 
MEVre : Flux du champ magnétique   31-12-20 à 11:46
MEV @ 31-12-2020 à 11:44

Pour ce carré ,  

et = (0.I)/2r suivant 
 Posté par 
vanoisere : Flux du champ magnétique   31-12-20 à 13:19
Bonjour

La méthode consiste à découper le rectangle en bandes élémentaires parallèles au fil créant le champ magnétique. Scanne un schéma précis.
 Posté par 
MEVre : Flux du champ magnétique   02-01-21 à 12:51
Bonjour Vanoise , Merci beaucoup pour votre intervention . J'ai dejà réussi à avoir l'expression du flux magnétique . 

J'ai trouvé : 

=(0I/2)a.ln[(D+a/2)/(D-a/2)]
 Posté par 
MEVre : Flux du champ magnétique   02-01-21 à 13:07
Méthode : 

=  



Avec =(0.I)/(2.x)z ( Champ crée par un fil infini à une distance x de son axe ici (Oy) ) il est dirigé ici dans ce cas par z



et =dS=dxdyz 



Pour les bornes d'intégration y varie de -a/2 à +a/2 et x varie de D-a/2 à D+a/2
 Posté par 
MEVre : Flux du champ magnétique   02-01-21 à 13:09
Voici le schéma ci-dessous



 Posté par 
vanoisere : Flux du champ magnétique   02-01-21 à 18:07
Bonsoir

 Merci pour le schéma. Commence par orienter ton cadre : le signe du flux dépend de cette orientation. Calcule ensuite le flux à travers une bande  parallèle au fil dont les cotés verticaux sont aux distances r et (r+dr) du fil. Reste ensuite à intégrer entre r=D-a/2 et r= D+a/2.
 Posté par 
vanoisere : Flux du champ magnétique   02-01-21 à 18:11
C'est bien ce que tu as fait dans ton message de 12h51. La valeur absolue que tu obtient est correcte. Reste le problème du signe du flux qui dépend du sens de circulation choisi le long du cadre.
 Posté par 
MEVre : Flux du champ magnétique   02-01-21 à 21:39
Pour le signe dont vous parlez J'ai omis quelque chose , il y'a un + du coté haut du carré 
 Posté par 
MEVre : Flux du champ magnétique   02-01-21 à 21:41
Je ne comprends pas Svp l'orientation est-elle vraiment indispensable ici ? 

C'est quoi son rôle svp ? Merci d'avance 
  Posté par 
vanoisere : Flux du champ magnétique   02-01-21 à 22:57
Citation :
l'orientation est-elle vraiment indispensable ici ?

L'orientation préalable du circuit filiforme fermé à travers lequel tu calcules un flux est toujours indispensable.

Repars pour t'en convaincre de l'expression du flux élémentaire :  .

Le sens de  est imposé par la source du champ magnétique (ici le conducteur parcouru par un courant continu). On sait aussi que le vecteur  est normal à la surface à travers laquelle on calcule le flux mais quel est le sens de ce vecteur ? Il est lié au sens de circulation choisi le long du contour délimitant la surface par la règle du tire-bouchon de Maxwell (ou tout autre règle équivalente).

Si tu choisis ici comme sens positif de circulation le long du carré le sens de rotation des aiguilles d'une montre, le vecteur  est orienté vers l'arrière de la figure, ce qui conduit ici à un flux positif. Si tu choisis comme sens positif le sens antihoraire (sens trigonométrique) le flux est négatif.