Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

flux de champ

Posté par
kamikaz 05-11-21 à 14:36

Bonsoir,

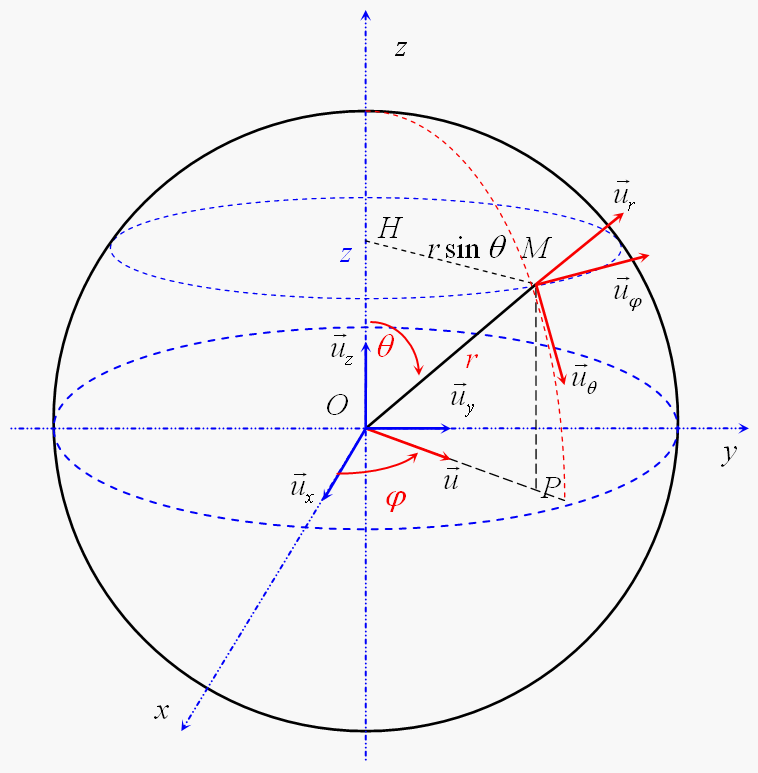
Un champ a la symétrie de révolution autour de l'axe Oz, de sorte que l'on se place dans un plan méridien. Dans ce plan, on adopte les coordonnées polaires avec Oz comme axe polaire ; le potentiel a alors comme expression : V= \dfrac{k(3 \cos ² \theta -1)}{r^3}.


1) Déterminer les composantes du champ \vec{E}
en utilisant les coordonnées polaires.

2) Calculer le flux \phi de ce champ à travers une calotte sphérique centrée en O, de révolution autour de Oz, et le rayon est « vu » du centre O sous l'angle \alpha. Déterminer \phi pour le cas particulier où \alpha = \pi

1) On a : \vec{E} = - \vec{{grad}} V

En coordonnées polaire (r ; \theta)  on a :

*E_r = - \dfrac{\partial V}{\partial r}= \dfrac{K}{r²} avec K= k(3 \cos²\theta -1)

*E_{\theta}= - \dfrac{\partial V}{\partial \theta}= \dfrac{3k \sin 2 \theta}{r}

2) On a : \phi = \dfrac{Q}{\epsilon _0}

Or \rho = \dfrac{dQ}{d V} \Rightarrow dQ = \rho dV

Pour la calotte dV = 2\pi r² \sin \alpha d\alpha

dQ =\rho 2\pi r² \sin \alpha d\alpha

Q= \int^{\alpha_0} _{0} \rho 2\pi r² \sin \alpha d\alpha

Q= 2\pi r² \rho (1- \cos \alpha)

\phi = \dfrac{2\pi r² \rho (1- \cos \alpha)}{\epsilon _0}

Pour \alpha = \alpha _0 = \pi on a : \phi = \dfrac{4\pi r² \rho}{\epsilon _0}

Posté par
vanoisere : flux de champ 05-11-21 à 14:46

Il faut que tu revois l'expression du gradient en coordonnées sphériques (voir par exemple le paragraphe 6 de ce document : ). L'expression que tu utilises n'est pas homogène.
Ensuite : attention à ne pas utiliser la même lettre V pour le potentiel électrostatique et le volume : on n'y comprends plus rien.
Pour la question 2 : le théorème de Gauss n'a aucun intérêt : on ne dispose pas d'une surface fermée. Il faut utiliser tout simplement la définition du flux d'un vecteur à travers une surface et appliquer la formule à une calotte sphérique. Il est intéressant d'utiliser les coordonnées sphériques.

Posté par
kamikazre : flux de champ 06-11-21 à 00:09

Ok mais je n'arrive pas à ouvrir votre lien

Posté par
vanoisere : flux de champ 06-11-21 à 14:00

Citation :
je n'arrive pas à ouvrir votre lien

Bizarre : pas de problème chez moi, ni sur mon pc, ni sur mon téléphone portable...
Tu retrouves la même fiche ici :
Les opérateurs en Sciences Physiques

Posté par
kamikazre : flux de champ 06-11-21 à 19:24

Citation :
Il faut que tu revois l'expression du gradient en coordonnées sphériques


Mais l'énoncé demande les composantes du champ \vec{E}
en utilisant les coordonnées polaires.

Posté par
vanoisere : flux de champ 06-11-21 à 22:02

Polaires : cas particulier de sphériques si =constante.
De toutes les façons, il faut utiliser les coordonnées sphériques puisqu'il est question ensuite de calotte sphérique.

Posté par
kamikazre : flux de champ 07-11-21 à 17:59

Ok

1) \vec{E} = \dfrac{k(3 \cos²\theta -1)}{r²} \vec{u_r}+\dfrac{3k \sin 2 \theta}{r²} \vec{u_{\theta}}

2)

Citation :
Il faut utiliser tout simplement la définition du flux d'un vecteur à travers une surface et appliquer la formule à une calotte sphérique. Il est intéressant d'utiliser les coordonnées sphériques.


J'ai pas compris.

\phi = \dfrac{q}{4\pi \epsilon_0 } \Omega

La surface n'étant pas fermée on \Omega \neq 4\pi

Pour une calotte sphérique on a : \Omega = \dfrac{S * \cos \alpha}{r²} avec S= 2\pi r² \sin \alpha

Donc \phi = \dfrac{q}{4\pi \epsilon_0 } *2\pi  \sin \alpha \cos \alpha = \dfrac{q}{4\pi \epsilon_0 }\sin 2\alpha  

\phi =\dfrac{q \sin 2\alpha}{4\pi \epsilon_0 } ; pour \alpha = \pi on a : \phi = 0

Posté par
vanoisere : flux de champ 07-11-21 à 18:08

Erreur sur l'expression du vecteur champ. Quelle formule utilises-tu pour passer du potentiel au vecteur champ ?
Tu es sûr de ne pas confondre dérivation et intégration ?

Il faut ensuite exprimer la surface élémentaire dS d'un petit élément de surface puis appliquer la formule :

\Phi=\iint_{calotte}\overrightarrow{E}.dS.\overrightarrow{u_{r}}

en utilisant les coordonnées sphériques.

Posté par
kamikazre : flux de champ 07-11-21 à 18:44

Citation :
Erreur sur l'expression du vecteur champ. Quelle formule utilises-tu pour passer du potentiel au vecteur champ ?


J'ai dérivé l'expression de V mais j'ai utilisé r au lieu de r3.


\vec{E} = \dfrac{3k(3 \cos²\theta -1)}{r^4} \vec{u_r}+\dfrac{3k \sin 2 \theta}{r²} \vec{u_{\theta}}


\Phi=\iint_{calotte}\overrightarrow{E}.dS.\overrightarrow{u_{r}}=\iint_{calotte}\left(\dfrac{3k(3 \cos²\theta -1)}{r^4} \vec{u_r}+\dfrac{3k \sin 2 \theta}{r²} \vec{u_{\theta}}\right).dS.\overrightarrow{u_{r}}

Comment effectuer ce calcul ?

Posté par
vanoisere : flux de champ 07-11-21 à 19:07

Ton expression du vecteur champ est nécessairement fausse car elle n'est pas homogène : on ne peut pas additionner un terme en k/r4 et un terme en k/r2.
La formule à utiliser est démontrée paragraphe 6 du document que je t'ai indiqué.

Posté par
kamikazre : flux de champ 08-11-21 à 04:18

Je ne vois pas vraiment..

Posté par
vanoisere : flux de champ 08-11-21 à 10:42

En adaptant la formule fournie sur mon document dans le cas des coordonnées sphériques :

\overrightarrow{E}=-\overrightarrow{grad}\left(V\right)=-\frac{\partial V}{\partial r}\cdot\overrightarrow{u_{r}}-\frac{1}{r}\cdot\frac{\partial V}{\partial\theta}\cdot\overrightarrow{u_{\theta}}-\frac{1}{r\cdot\sin\left(\theta\right)}\cdot\frac{\partial V}{\partial\varphi}\cdot\overrightarrow{u_{\varphi}}
Ici : le potentiel V ne dépend pas de l'angle ; la troisième composante du vecteur champ est donc nulle.

flux de champ

Posté par
kamikazre : flux de champ 09-11-21 à 10:16

\vec{E}= \dfrac{3k(3 \cos ² \theta -1)}{r^4}\vec{u_r}+\dfrac{3k \sin 2\theta}{r^4} \vec{u_\theta}

Posté par
vanoisere : flux de champ 09-11-21 à 10:56

D'accord avec ton expression du vecteur champ.
Je t'ai fournie l'expression générale du flux de ce vecteur à travers une surface.Seule la composante normale à la surface intervient : ici Er.
Puisque Er ne dépend pas de , tu peux commencer par calculer le flux élémentaire dΦ à travers la couronne élémentaire  de rayon HM=R.sin() et de largeur élémentaire R.d.
Il suffit ensuite d'intégrer par rapport à entre =0 et =.

Posté par
kamikazre : flux de champ 09-11-21 à 18:03

\phi = \int ^{\alpha} _{0} \dfrac{3k(3 \cos² \theta -1)}{r^4} dS

d \phi =\dfrac{3k(3 \cos² \theta -1)}{r^4} ×S

d \phi = \dfrac{3k(3 \cos² \theta -1)}{r^4} ×2\pi R² \sin \theta

d \phi = \dfrac{6\pi k R² \sin \theta (3 \cos² \theta -1)}{r^4}

Posté par
vanoisere : flux de champ 09-11-21 à 18:23

Tu ne maîtrises pas l'écriture différentielle : une différentielle (dΦ par exemple) doit s'écrire sous la forme f(θ).dθ ... De plus, je ne suis pas certain que tu aies bien compris ce que représente le flux d'un vecteur à travers une surface ; Le vecteur dont on calcule le flux est le vecteur définie en tout point de la surface, donc ici le vecteur champ en r= R. De plus, seule la composante du vecteur, normale en tout point à la surface, intervient dans le calcul.

d\Phi=E_{r}.2\pi.R^{2}.\sin\left(\theta\right).d\theta=\frac{6\pi.k}{R^{2}}\cdot\left[3\cos^{2}\left(\theta\right)-1\right]\cdot\sin\left(\theta\right)\cdot d\theta

\Phi=\frac{6\pi.k}{R^{2}}\cdot\int_{0}^{\alpha}\left[3\cos^{2}\left(\theta\right)-1\right]\cdot\sin\left(\theta\right)\cdot d\theta

Posté par
kamikazre : flux de champ 09-11-21 à 19:13

Où est passé le r⁴ ?

Posté par
vanoisere : flux de champ 09-11-21 à 19:40

Tu n'as pas bien compris mon message précédent concernant la définition du flux et l'égalité qui en résulte  : r = R.

Posté par
kamikazre : flux de champ 10-11-21 à 13:48

\phi = \dfrac{6 \pi k}{R²}(\cos \alpha -\cos ^3 \alpha )

Posté par
vanoisere : flux de champ 10-11-21 à 13:55

C'est cela ! Reste à traiter le cas particulier de la sphère.

Posté par
kamikazre : flux de champ 10-11-21 à 14:57

Comment çà ?

Posté par
vanoisere : flux de champ 10-11-21 à 15:28

À quoi correspond selon toi le cas = ?

Posté par
kamikazre : flux de champ 11-11-21 à 13:24

Ah ok je ne l'avais pas compris ainsi.

Pour \alpha = \pi ; \phi = \dfrac{6 \pi k}{R²}(\cos \pi -\cos ^3 \pi ) = 0

Posté par
vanoisere : flux de champ 11-11-21 à 13:45

C'est bien cela ! Petite question de réflexion, si tu as le temps : quelle est la charge totale qui crée le champ étudié ici  à ton avis ?

Posté par
kamikazre : flux de champ 11-11-21 à 23:27

La circulation C= \int \phi (u) du et C = \int \vec{V} (M) \vec{dM}

Donc \phi (u) = V(M)= \dfrac{Q}{4\pi \epsilon_0 r} avec \phi =0

\dfrac{Q}{4\pi \epsilon_0 r}= 0

Q=0

La charge totale ici est donc nulle.

Posté par
vanoisere : flux de champ 12-11-21 à 15:05

Citation :
La charge totale ici est donc nulle.

C'est bien cela. En fait, la source qui crée un tel champ est un dipôle électrostatique centré en O. Un tel dipôle est un ensemble de deux charges ponctuelles q et -q situées toutes deux très près du point O.

Posté par
kamikazre : flux de champ 12-11-21 à 18:21

J'ai pas compris pourquoi..

Posté par
vanoisere : flux de champ 12-11-21 à 18:23

Cela n'est pas nécessaire à la compréhension de cet exercice. C'est juste un complément d'information au cas où tu aurais déjà étudié les dipôles électrostatiques. Si ce n'est pas le cas, laisse tomber...

Posté par
kamikazre : flux de champ 12-11-21 à 20:19

D'accord, merci beaucoup


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !