Inscription / Connexion Nouveau Sujet
Flux
etudiantilois
Bonsoir,
J'ai des difficultés avec l'exercice ci-dessous. Je pense avoir réussi la question 2, mais comment faire pour la question 1 ? Merci beaucoup d'avance pour l'aide.
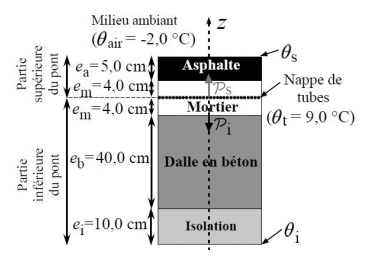
Des chercheurs allemands ont développé un nouveau procédé de chauffage qui permet de réduire fortement la formation de verglas sur les ponts. Un circuit hydraulique d'eau chaude alimente une « nappe » de tubes, intégrée au revêtement d'asphalte du pont pour empêcher la formation de verglas en hiver. La surface de la chaussée à dégivrer est S=1300 m². Le transfert thermique est considéré comme unidirectionnelle d'axe (Oz) et le régime est stationnaire.
La température au niveau de la nappe de tubes Tt est différente de celle de l'air, Tair. Le pont est le siège d'un flux thermique Ps dans la partie supérieure et Pi dans la partie inférieure.
Du fait du phénomène de convection, les températures des surfaces inférieures et supérieure, respectivement Ti et Ts et ne sont pas égales à la température de l'air ambiant, elles vérifient la loi de Newton, exprimée ci-dessous pour chacune des températures :
Ps=hS(Ts-Tair).
Pi=hS(Ti-Tair).
Avec h coefficient de convection : h=10,0 W.K-1m-2.
Données :
Conductivités thermiques :
Du béton : 
bé=2,1 W.K-1m-1
De l'asphalte : a=4,0 W.K-1m-1
Du mortier : m=2,4 W.K-1m-1
De l'isolation : i=0,0056 W.K-1m-1
1. Montrer que la loi de Newton permet de définir une résistance thermique par convection Rth,conversion=1/hS.
2. Exprimer la résistance thermique Rs équivalente à l'ensemble de la partie supérieure tenant compte de la conduction dans le pont et de la convection dans l'air.
3. Donner l'expression du flux thermique Ps en fonction de la température au niveau de la nappe de tubes Tt, de la température de l'air Tair et de la résistance Rs.
4. En déduire l'expression de la température Ts en fonction des données de l'énoncé et déterminer la température 
s en degré Celsius. Conclure sur l'efficacité du système de chauffage quant à son objectif.
5. À l'aide d'un raisonnement similaire à celui des questions 3, 4 et 5, déterminer la température de la surface inférieure du pont, i. Justifier la cohérence de la valeur obtenue.
Bonjour
À la différence de potentiels (tension électrique) en électricité correspond ici la différence de températures 
T. À l'intensité électrique correspond ici le flux thermique (ou puissance thermique) Pth .
Par analogie avec la loi d'Ohm, on pose donc ici :
T=Rth . Pth
Merci beaucoup pour votre réponse.
Elle concerne la question 1 ou la question 2 ?
Parce que si ce que vous avez écrit concerne la question 1, je ne vois pas comment la terminer...
Ma réponse concerne d'abord la première question mais elle va être utile dans tout le problème car il s'agit ici de raisonner par analogie avec les circuits électriques sur les associations en série ou en parallèle de résistances thermiques.
As-tu bien étudié ton cours sur ce sujet ?
Merci, je viens de comprendre votre message de 12h13 !
Je comprends bien l'analogie avec l'électricité et j'ai revu l'association en série, en parallèle...
Mais donc comment faire la question 1 avec cette analogie ? Parce que je ne vois pas trop...
Merci de m'avoir signalé cette analogie en tout cas !
La résistance supérieure est équivalente à l'association en série de trois résistances :
- celle de 4cm de mortier
- celle de 5cm d'asphalte
- celle due au phénomène de convection définie à la question précédente.
Raisonnement analogue pour la résistance inférieure...
Mais alors ce que vous me dites est pour la question 2 ?
Je suis désolé, je ne comprends pas...
Parce que la résistance supérieure est équivalente à la somme des 3, mais comment les écrire ? Et quoi faire pour la 1 ?
Merci encore pour l'aide.
J'ai déjà pu te l'écrire lorsqu'on avait fait un exercice sur les oscillations forcées, on ne peut pas se lancer tête baissée dans un exercice sans maîtriser son cours ...
Comme te l'as rappelé vanoise (que je salue à mon tour), tu dois de nouveau faire une analogie électrique : 
Ta résistance équivalente est une association de résistances thermiques tenant compte de deux phénomènes :
- transfert thermique (cf. la formule que je t'ai rappelée dans ton autre exercice) ;
- transfert conducto-convectif dont la formule est donnée dans l'énoncé.
A partir de ce schéma :
Essaie de faire un schéma d'analogie électrique avec les données fournies par l'énoncé
J'ai compris la question 1, ça y est !
Par contre, pour la question 2, comme on est en série, on aura effectivement la somme des résistances liées à la convection et à la conduction.
Dans mon cours, il y a la formule suivante :
Pour un conducteur de longueur l, de section constante S et de conductivité thermique (en W.K-1.m-1) :
Rth=l/S.
Pour la question 2 :
On aurait donc, comme on est en série :
Rth=1/hS (trouvé à la question 1) + ea/(asphalte*S) + em/(mortier*S).
Est-ce correct ?
Je pense que non, car j'ai trouvé un site Internet avec quasiment le même exercice. Voici l'énoncé (page 6) :
Et le corrigé (page 5) :
Dans ce corrigé, il est plutôt écrit :
Rth=1/h+ ea/asphalte + em/mortier
Alors, je ne comprends pas, y a-t-il un S au dénominateur ?
Si non, pourquoi n'y en aurait-il pas ?
Merci encore pour l'aide.
Annuler
connectez vous