filtre second ordre, exercice de Physique

 Niveau école ingénieurPartager :
			        
					
				
filtre second ordre
Posté par 
Meedfried  21-12-21 à 18:09
Bonjour,



J'ai une petite question sur les filtres second ordre. 

J'ai un filtre R et C en parallèles avec L en série. 

On a donc 



On peut transformer cette expression avec wo et Q. Cependant, on nous a dit que wo ou fo qui est la fréquence propre était la fréquence de coupure du filtre. Pour moi cela est faux !! Pour trouver la fréquence de coupure, on doit résoudre le système avec Vs/Ve = 0.7071 (-3dB)



Merci !
 Posté par 
vanoisere : filtre second ordre  21-12-21 à 18:30
Bonjour 

Tu as raison. o est la pulsation propre.  Comme tu l'écris, la ou les pulsations de coupure correspond(ent) à 

GdB = Gmax - 3

en dB.
 Posté par 
Meedfriedre : filtre second ordre  21-12-21 à 19:05
Merci, 

Mais alors pourquoi sur internet il considère aussi  Wc = Wn (la fréquence propre) ?



Et enfin, l'équation à résoudre me parait compliquer à résoudre car en module, on a du w puissance 4 ... 
 Posté par 
vanoisere : filtre second ordre  21-12-21 à 21:54
Citation :
Mais alors pourquoi sur internet il considère aussi  Wc = Wn (la fréquence propre) ? 

Je t'ai indiqué les conventions les plus courantes en France mais il s'agit de conventions...

Citation :
l'équation à résoudre me parait compliquer à résoudre car en module, on a du w puissance 4 ... 

Les calculs sur les filtres du second ordre deviennent plus faciles en adoptant pour le dénominateur la forme normalisée suivantes :




avec :  et  une constante dépendant des composants du filtres. Pour les passe-bandes notamment, il peut être intéressant d'introduire le facteur de qualité du filtre :  .
 Posté par 
vanoisere : filtre second ordre  22-12-21 à 14:12
Citation :
l'équation à résoudre me parait compliquer à résoudre car en module, on a du w puissance 4 ... 

Moins compliqué qu'il n'y parait car poser X=x2 ramène à une équation du deuxième degré sans introduire d'ambiguïté de signe puisque  , et donc aussi x, sont des grandeurs strictement positives.
 Posté par 
Meedfriedre : filtre second ordre  22-12-21 à 19:13
Merci,

Mais est ce une bonne approximation si on considère Wn = Wc ?

(je n'ai pas trop compris). 

On a donc dans ce cas 

wo = 1/ racine(LC) et beta = (L wo ) / (2R) 
 Posté par 
vanoisere : filtre second ordre  22-12-21 à 22:17
Oui !

Citation :
Mais alors pourquoi sur internet il considère aussi  Wc = Wn (la fréquence propre) ? 

Je n'ai pas la référence précise de l'article que tu évoques...
 Posté par 
Meedfriedre : filtre second ordre  23-12-21 à 14:27
Je parle de cette article : http://www.specialautom.net/freq-deuxieme-ordre.htm



 Posté par 
vanoisere : filtre second ordre  23-12-21 à 15:21
Ce document est clair et bien présenté. Il utilise des notations tout à fait cohérentes mais pas nécessairement les plus fréquentes. A ce que je comprends :

n correspond au classique o.

le paramètre "z" est ce que j'ai appelé précédemment .

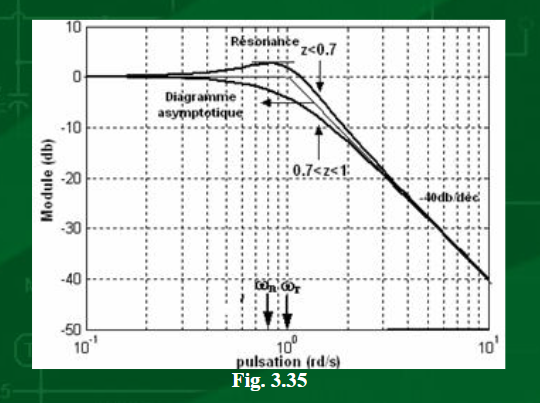
r correspond à G=Gmax : cela correspond à la pulsation de résonance de charge dans le cas d'un passe-bas du second ordre de type RLC.

c ne désigne pas une pulsation critique mais une pulsation de cassure correspondant à une "cassure" ou rupture de pente du diagramme asymptotique. Pour les valeurs de =z<1, le diagramme asymptotique correspond à une horizontale et à une oblique de pente -20dB par décade qui se coupent en  c=o.
  Posté par 
Meedfriedre : filtre second ordre  23-12-21 à 16:26
Merci, 

Donc le mieux est de vérifier z en le calculant et donc utiliser le fait que wo=wc pour z<1 (plus simple )