Inscription / Connexion Nouveau Sujet
Filtre RLC sélectif réjecteur de bande
Bonjour , je suis bloqué sur un exo:
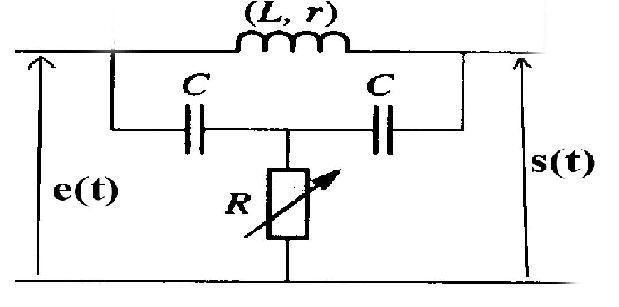
Le filtre représenté ci-dessus est constitué:
- d'une résistance R variable
- de deux capacités identiques C
- d'une bobine d'inductance propre : L et de résistance r.
Ce filtre est alimenté à l'entrée, par une tension sinusoïdale v1 de
fréquence f=
/(2
) variable. La sortie du filtre est en circuit ouvert.
1°) Pour quelle valeur R1 de la résistance variable et pour quelle fréquence f0=0/(2) la
tension de sortie est-elle nulle?
-- Je bloque sur cette question , je ne sais pas par où commencer . ( en toute logique il faut que l'impédance du système soit infini et qu'on se trouve à une pulsation d'antirésonance mais bon j'ai du mal a être autonome en élec ...)
2°) Exprimer la fonction de transfert (lorsque R=R0) du filtre .
-- j'ai fait quelque chose en utilisant la transformation de Kenelly , mais je ne suis vraiment pas sûr .. existe t'il une autre méthode ?
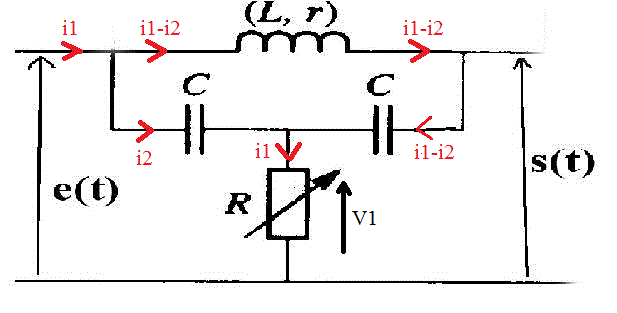
e - s = (r + jwL).(i1-i2)
i2 = jwC(e - V1)
i1 = V1/R
(i1-i2) = jwC(s - v1)
e - s = (r + jwL).(V1/R - jwC(e - V1))
R(e - s) = (r + jwL).(V1 - jwRC(e - V1))
R(e - s) = V1.(r + jwL)(1 + jwRC) - e.jwRC(r+jwL)
R(e - s) + e.jwRC(r+jwL) = V1.(r + jwL)(1 + jwRC)
(V1/R - jwC(e - V1)) = jwC(s - v1)
(V1 - jwRC(e - V1)) = jwRC(s - v1)
V1(1 + 2jwRC) = jwRC(s + e)
V1 = jwRC(s + e)/(1 + 2jwRC)
R(e - s) + e.jwRC(r+jwL) = (r + jwL)(1 + jwRC).jwRC(s + e)/(1 + 2jwRC)
R(e - s)(1 + 2jwRC) + e.jwRC(r+jwL)(1 + 2jwRC) = (r + jwL)(1 + jwRC).jwRC(s + e)
e.[R.(1 + 2jwRC) + jwRC(r+jwL)(1 + 2jwRC) - (r + jwL)(1 + jwRC).jwRC] = s.[R.(1 + 2jwRC) + (r + jwL)(1 + jwRC).jwRC]
e.[R.(1 + 2jwRC).(1 + jwC(r+jwL)) - (r + jwL)(1 + jwRC).jwRC] = s.[R.(1 + 2jwRC) + (r + jwL)(1 + jwRC).jwRC]
s = 0 pour [R.(1 + 2jwRC).(1 + jwC(r+jwL)) - (r + jwL)(1 + jwRC).jwRC] = 0
R + 2jwR²C + jwCRr + j²w²RLC + 2j²w²R²C²r + 2j³w³R²C²L - jwRCr - j²w²R²rC² - j²w²LRC - j³w³LR²C² = 0
R + 2jwR²C + j²w²R²C²r + j³w³R²C²L = 0
1 + 2jwRC + j²w²RC²r + j³w³RC²L = 0
1 + R(2jwC - w²C²r - j.w³C²L) = 0
R = 1/(w²C²r + j(w³C²L - 2wC)) = 0
R réel --> (w³C²L - 2wC) = 0 (pour w différent de 0)
w²CL = 2
w² = 2/(LC)
w = V[2/(LC)]
R = 1/(w²C²r)
R = LC/(2C²r)
R = L/(2rC)
wo = V[2/(LC)]
R1 = L/(2rC)
-----
Naturellement sans aucune vérification ... et donc probablement avec des erreurs de calcul.
Vérifie.
Annuler
connectez vous