Inscription / Connexion Nouveau Sujet
Filtre Passif de Hartley
Bien le bonsoir, c'est le printemps et les affaires reprennent.
j'ai là un petit sujet qui me cause bien du souci. je fais donc appel à votre expertise.
Il s'agit d'étudier un filtre du type Hartley utilisé dans la réalisation de l'oscillateur à transistor du même nom (fig. 2).
Sa structure électronique est donnée ci-contre.
a est un coefficient réel positif.
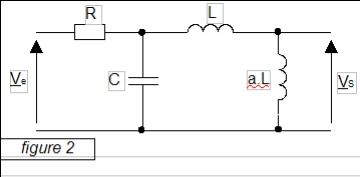
2.1. Déterminer l'expression de la fonction de transfert isochrone T(jw)=Vs/Ve du filtre.
Montrer que l'on peut l'écrire sous la forme :
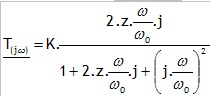
Donner les expressions de K en fonction de a, de z en fonction de R, L, C et a et W0 en fonction de L, C et a.
2.2. On souhaite avoir z = 2 et W0 = 10000 rad/s avec L = 220 mH et C = 10 nF.
Quelles valeurs faut-il donner à R et a ?
2.3. Compte tenu de la valeur de z, montrer que la fonction de transfert peut également s'écrire sous la forme :.
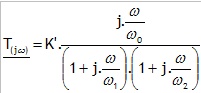
Donner les expressions de K', W1 et W2. Calculer K', W1 et W2.
2.4. Pour la suite on prendra K' = 3,12. Tracer les diagrammes asymptotiques de gain et phase sur le document réponse 2. On précisera les pentes des asymptotes.
2.5. Tracer les courbes réelles de gain et de phase. On choisira judicieusement quelques points pour lesquels on regroupera les calculs dans un tableau.
2.6. Quel est le type de ce filtre ?
pour la question 2.1 : je trouve
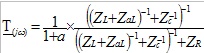 donc
donc 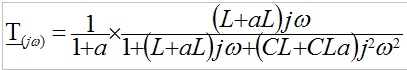
d'où
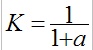 ;
;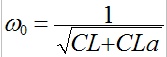 ;
;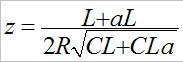
question 2.2
a=3.5454
R=2.5 kOhms
question 2.3
là je sèche... j'ai posé les deux expressions de part et d'autre d'une égalité, développé, factorisé... tout ça pour tourner en rond...
je suis quand même arrivé à supposer que K'=4K
Bonjour, sauf erreur de ma part, tu ne peux pas factoriser le dénominateur ? (avec discriminant puis calcul des racines )
Bonjour à tous les deux,
Emouchet >>
Bienvenue sur l'  pour ton premier problème !
pour ton premier problème !
Mais deux remarques :
. tu peux attacher des images à la condition de respecter la FAQ, en l'occurrence ici, en les plaçant sur le serveur de l'  ; relis la procédure :
; relis la procédure : 
![]() [lien]
[lien]
. les expressions algébriques n'ont pas à être postées sous la forme d'images ; le site permet l'usage d'un LaTeX avec lequel tu peux écrire toutes ces expressions avec la même qualité graphique.

Je n'ai pas la même chose pour les premières questions. (Mais je n'ai pas vérifié mes calculs)
2.1
z1 = C en // sur (L + aL)
z1 = jwL(a+1)/(1 + j²w²LC(a+1))
Avec v1 la tension su C :
Ve/(R+z1) = V1/z1 et vs/a = V1/(a+1) -->
vs/ve = [a/(a+1)].z1/(R+z1)
Après simplification, on a :
vs/ve = [a/(a+1)].jwL/[R + j²w²LC(a+1)R + jwL]
vs/ve = [a/(a+1)].jw(L/R)/[1 + j²w²LC(a+1) + jw(L/R)]
A la résonance, on a : 1 + j²wo²LC(a+1) = 0
Soit wo = 1/V((a+1).LC)
Et donc :
vs/ve = [a/(a+1)].(jwL/R)/[1 + jwL/R + j²w²LC(a+1)]
vs/ve = [a/(a+1)].(jwL/R)/[1 + jwL/R + (jw/wo)²]
En posant a/(a+1) = K et L/R = 2Z/wo, il vient :
vs/ve = K.2.Z.(w/wo).j/[1 + 2.z.(w/wo).j + (jw/wo)²]
Qui est l'expression à trouver dans la question 2.1
Cette expression est valable avec :
K = a/(a+1)
wo = 1/V((a+1).LC)
L/R = 2Z/wo
-----
2.2
K = a/(a+1)
wo = 1/V((a+1).LC)
L/R = 2Z/wo
K = a/(a+1)
10000 = 1/V((a+1).0,22*10^-8)
0,22/R = 4/10000
R = 550 ohms
a = 3,5454...
K = 0,78
-----
2.3
Compte tenu que Z = 2 et K = 0,78
Vs/Ve = K.2.Z.(w/wo).j/[1 + 2.z.(w/wo).j + (jw/wo)²]
Vs/Ve = 4*0,78 .(w/wo).j/[1 + 2*2.(w/wo).j + (jw/wo)²]
Vs/Ve = 3,12 .(w/wo).j/[1 + 4.(w/wo).j + (jw/wo)²]
Et donc K' = 3,12
Racines de : 1 + 4.(w/wo).j + (jw/wo)²
...
1 + 4.(w/wo).j + (jw/wo)² = (1 + j(w/wo)/(2-V3)). (1 + j(w/wo)/(2+V3))
et en posant (2-V3)wo = w1 et (2+V3)wo = w2, on a :
1 + 4.(w/wo).j + (jw/wo)² = (1 + j(w/w1)). (1 + j(w/w2))
-->
Vs/Ve = 3,12 .(w/wo).j/[(1 + j(w/w1)).(1 + j(w/w2))]
Avec K' = 3,12 , (2-V3)wo = w1 et (2+V3)wo = w2
-----
Sauf distraction. 


