Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

Filtre passif

Posté par
Physical111 28-03-23 à 19:22

Bonjour à tous
J'ai un exercice merci beaucoup d'avance
•On considère le filtre suivant, alimenté par une tension alternative sinusoïdale de pulsation
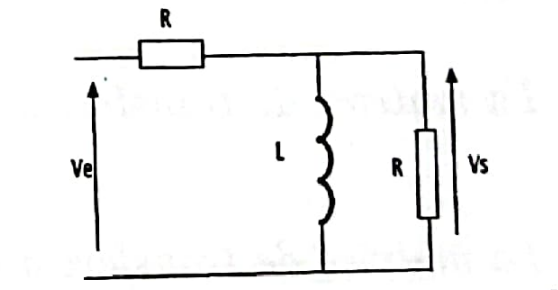
Filtre passif
1) faire une étude du comportement asymptotique pour déterminer le type de ce filtre
2) Montrer que T(j)=\dfrac{1}{T_{22}}
3) En s'inspirant de l'exercice précédent (question 1) déterminer la fonction de transfert de ce filtre et la mettre sous forme canonique
T(j)=T0\dfrac{j\dfrac{\omega}{\omega_0}}{1+j\dfrac{\omega}{\omega_0}}
Avec 0=\dfrac{R}{2L}
- Préciser la signification et la valeur de T0
4) Tracer la courbe de réponse en gain (GdB) dans le diagramme de Bode , en prenant pour abscisse x=/0 . Indiquer sur le graphique les pulsations de coupure
5) A l'aide de ces diagramme de Bode, déterminer Vs(t) lorsque Ve(t)=0.5cos(10t) . Justifier la méthode utilisée. On donne R=20 et L=0,01H
---------------------------------------
Alors je propose :
1)
A basse fréquence --->0
ZL=jL--->0 dans la bobine se comporte comme un file fermé
Donc on remplace ZL par un fil donc Vs=0
•au haute fréquence -->
Donc ZL -->
Donc la bobine se comporte comme un circuit ouvert
Donc dans ce cas Vs=Ve
Donc il s'agit d'un filtre pass haut ;les basses fréquence sont éliminés il laisse passer juste les tensions de haute fréquence
2)
T(j)=\dfrac{V_s}{V_e} (complexe)
Or \dfrac{1}{T_{22}}=\dfrac{-I_1}{I_2} lorsque V1=0
V1 ici c'est Ve
•T(j)=\dfrac{R}{R+Z_L}
Une indication s'il vous plaît merci beaucoup d'avance

Posté par
vanoisere : Filtre passif 28-03-23 à 21:34

Bonsoir

D'accord concernant le comportement asymptotique. Le filtre est en fait le quadripôle de l'exercice précédent. La fonction de transfert est, par définition :

T_{(j\omega)}=\frac{V_{s}}{V_{e}} dans le cas particulier : Is=0

Avec les notations des exercices précédents :

T_{(j\omega)}=\frac{V_{2}}{V_{1}} dans le cas particulier : I2=0

Le plus direct pour obtenir la fonction de transfert consiste à considérer que R et Ze se comporte en diviseur de tension :

T_{(j\omega)}=\frac{Z_{e}}{R+Z_{e}}

Posté par
Physical111re : Filtre passif 28-03-23 à 22:28

Bonjour
D'accord
T(j)=\dfrac{RjL\omega}{R+jL\omega}*\dfrac{1}{R+\dfrac{RjL\omega}{R+jL\omega}}=\dfrac{RjL\omega}{\left(R+jL\omega \right)\left(\dfrac{R²+RjL\omega+RjL\omega}{R+jL\omega} \right)}=\dfrac{RjL\omega}{R²+2RjL\omega}=[tex]\dfrac{RjL\omega}{R²\left( 1+2\dfrac{1}{R}jL\omega\right)}=\dfrac{j\dfrac{L}{R}\omega}{1+2\dfrac{L}{R}j\omega}
[/tex]
Mais je trouve pas 1/T22

Posté par
vanoisere : Filtre passif 28-03-23 à 23:00

D'accord avec ton expression de la fonction de transfert.

Citation :
Mais je trouve pas 1/T22

Moi non plus ! Si on tient effectivement à relier la fonction de transfert à la matrice de transfert, il faut utiliser la définition que j'en avait donnée (je mets des « ' » aux coefficients car ce ne sont pas ceux de ton cours) :

\left(\begin{array}{c} \\ \\ \\ V_{1}\\ \\ \\ \\ I_{1} \\ \end{array}\right)=\left(\begin{array}{cc} \\ \\ \\ T'_{11} & T'_{12}\\ \\ \\ \\ T'_{21} & T'_{22} \\ \end{array}\right)\left(\begin{array}{c} \\ \\ \\ V_{2}\\ \\ \\ \\ -I_{2} \\ \end{array}\right))

et alors :

T_{(j\omega)}=\frac{V_{2}}{V_{1}} dans le cas particulier : I2=0, soit : T_{(j\omega)}=\frac{1}{T'_{11}}.

On peut aussi remarquer que la fonction de transfert s'exprime directement en fonction d'un coefficient de la matrice hybride inverse : T_{(j\omega)}=g_{21}. Mais franchement : la notion de diviseur de tension est bien plus simple quand il s'agit de trouver une fonction de transfert. Les matrices de transferts sont vraiment intéressantes pour étudier une cascade de plusieurs quadripôles.

Posté par
Physical111re : Filtre passif 28-03-23 à 23:59

Bonjour
J'ai utilisé une autre alternative :
On a V2=T11V1-T12I1
I2=0=T21V1-T22I1
Donc I1=\dfrac{T_{21}V_1}{T_{22}}
En remplace dans la première équation:
V_2=\dfrac{T_{11}T_{22}-T_{12}T_{21}}{T_{22}}V_1
•T(j)=\dfrac{V_2}{V_1}=\dfrac{T_{11}T_{22}-T_{12}T_{21}}{T_{22}}
Donc il faut monter que le numérateur vaut 1
Or d'après l'exercice précédent :
[T]=\left(\begin{array}{cc} \\ 1 & R\\ \\ \dfrac{R+Z_L}{R*Z_L} & \dfrac{R+Zeq}{Zeq} \end{array}\right)
Or ce quadripole est passif alors ∆t=1
D'où \boxed{T(j\omega)=\dfrac{1}{T_{22}}}
Mais par un calcul du déterminant on trouve pas 1
•T0=Tmax=1 représente un gain maximal en décibel nul
Et on trouve pas que 0=R/2L
Merci beaucoup

Posté par
vanoisere : Filtre passif 29-03-23 à 11:04

Citation :
Mais par un calcul du déterminant on trouve pas 1 .


La matrice de transfert obtenue dans l'exercice précédent vérifie :

\left(\begin{array}{c} \\ v_{2}\\ \\ i_{2} \\ \end{array}\right)=\left(\begin{array}{cc} \\ 1 & R\\ \\ \frac{1}{Z_{e}} & \frac{R+Z_{e}}{Z_{e}} \\ \end{array}\right)\left(\begin{array}{c} \\ v_{1}\\ \\ -i_{1} \\ \end{array}\right)

Cela conduit bien à T=1 et on remarque effectivement :

T_{22}=\frac{R+Z_{e}}{Z_{e}}=\frac{1}{T_{(j\omega)}}

Pour la suite : petite astuce : multiplier la fonction de transfert par 2x(1/2) ne modifie pas sa valeur :

T_{(j\omega)}=\dfrac{1}{2}\cdot\dfrac{2\frac{jL\omega}{R}}{1+2\frac{jL\omega}{R}}

La suite est facile !

Posté par
Physical111re : Filtre passif 29-03-23 à 13:02

Bonjour
Oui effectivement ∆t=1
T_{(j\omega)}=\dfrac{1}{2}\cdot\dfrac{2\frac{jL\omega}{R}}{1+2\frac{jL\omega}{R}}=T_0\dfrac{j\dfrac{\omega}{\omega_0}}{1+j\dfrac{\omega}{\omega_0}}
Avec T0=\dfrac{1}{2}et 0=\dfrac{R}{2L}
la signification de T0
La valeur de T0 correspond à un gain maximal en décibel de 20log(1/2)
Merci beaucoup

Posté par
Physical111re : Filtre passif 29-03-23 à 20:06

Si c'est juste :
pour la 4)
On a T(j)=\dfrac{1}{2}\dfrac{jx}{1+jx}
Donc |T(j)|=\dfrac{1}{2}\dfrac{x}{\sqrt{1+x²}}
•GdB=20*log(|T(j)|=20 log(x)-20log(2\sqrt{1+x²}
)
•les asymptotes :
*En Basse fréquence (BF) x<<1 donc Gdb=20log(x)-20log(2)
*En haut fréquence x>>1 Gdb=20log(x)-20log(2x)
Une indication s'il vous plaît merci beaucoup d'avance

Posté par
vanoisere : Filtre passif 29-03-23 à 23:20

Il faut, autant que possible, s'arranger pour que x n'apparaisse qu'au dénominateur ; cela s'obtient en divisant tous les termes par jx :

T_{(j\omega)}=\dfrac{\frac{1}{2}}{1-\frac{j}{x}}

Le module du complexe est :

|T_{(j\omega)}|=\dfrac{\frac{1}{2}}{\sqrt{1+\frac{1}{x^{2}}}}

G_{(dB)}=-20\log\left(2\right)-10\log\left(1+\frac{1}{x^{2}}\right)\approx-6,0-10\log\left(1+\frac{1}{x^{2}}\right)

Les équations des asymptotes correspondent aux deux cas suivants :

1° : fréquences très inférieures à la fréquence de coupure : \frac{1}{x^{2}}\gg1

2° : fréquences très supérieures à la fréquence de coupure : \frac{1}{x^{2}}\ll1

Je te laisse continuer...

Posté par
Physical111re : Filtre passif 30-03-23 à 13:23

Bonjour
1° : fréquences très inférieures à la fréquence de coupure : \frac{1}{x^{2}}\gg1
donc : GdB=-6dB-10log(1/x2)=-6dB+20log(x)
C'est une droite oblique de +20dB/décade
2° : fréquences très supérieures à la fréquence de coupure : \frac{1}{x^{2}}\ll1
donc Gdb=-6db
C'est une droite horizontal
Le diagramme de bode pour le gain correspond à :
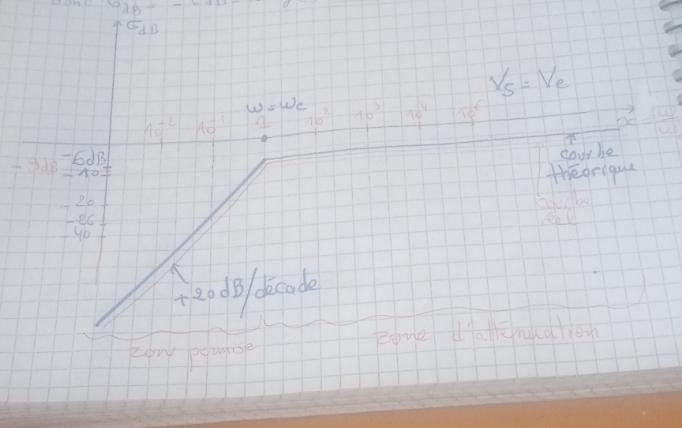
Filtre passif
•on a G(=0)=Gmax-3dB
•|T()|=\dfrac{T_0}{\sqrt 2}
J'espère que j'ai pas oublié quelque chose.
5) une indication s'il vous plaît merci beaucoup d'avance

Posté par
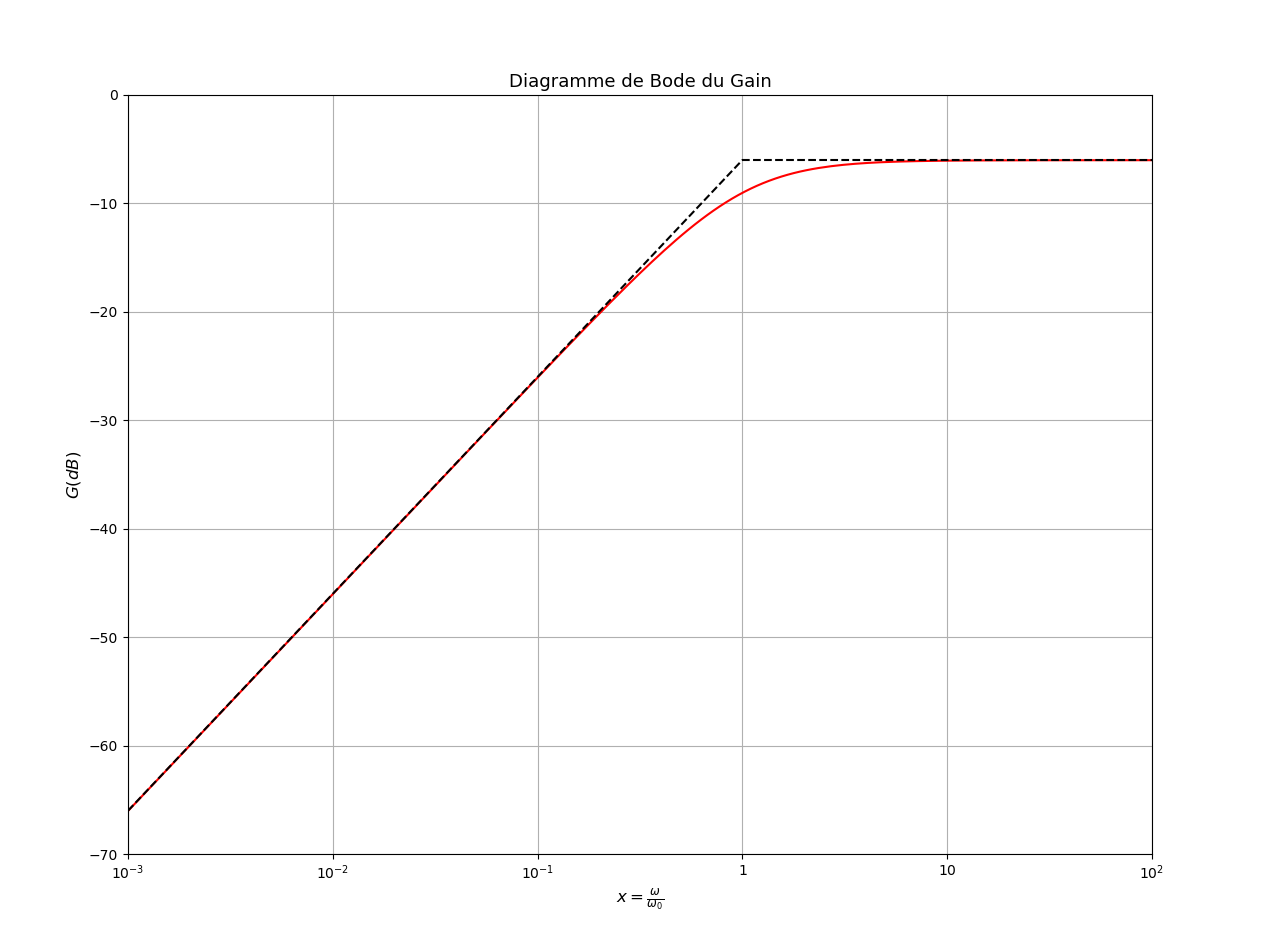
vanoisere : Filtre passif 30-03-23 à 14:23

Ensemble globalement correct. Attention tout de même : le diagramme théorique n'est pas le diagramme asymptotique mais la courbe tracée ci-dessous en rouge. Aucune expérience n'a été faite ici !
Pour f>>fo : ve=vs/2
Pour un filtre du premier ordre, c=o
Question 5 : Tu peux calculer numériquement x=/o.
Le rapport des amplitudes \frac{V_{Smax}}{V_{Emax}} est le module de la fonction de transfert.
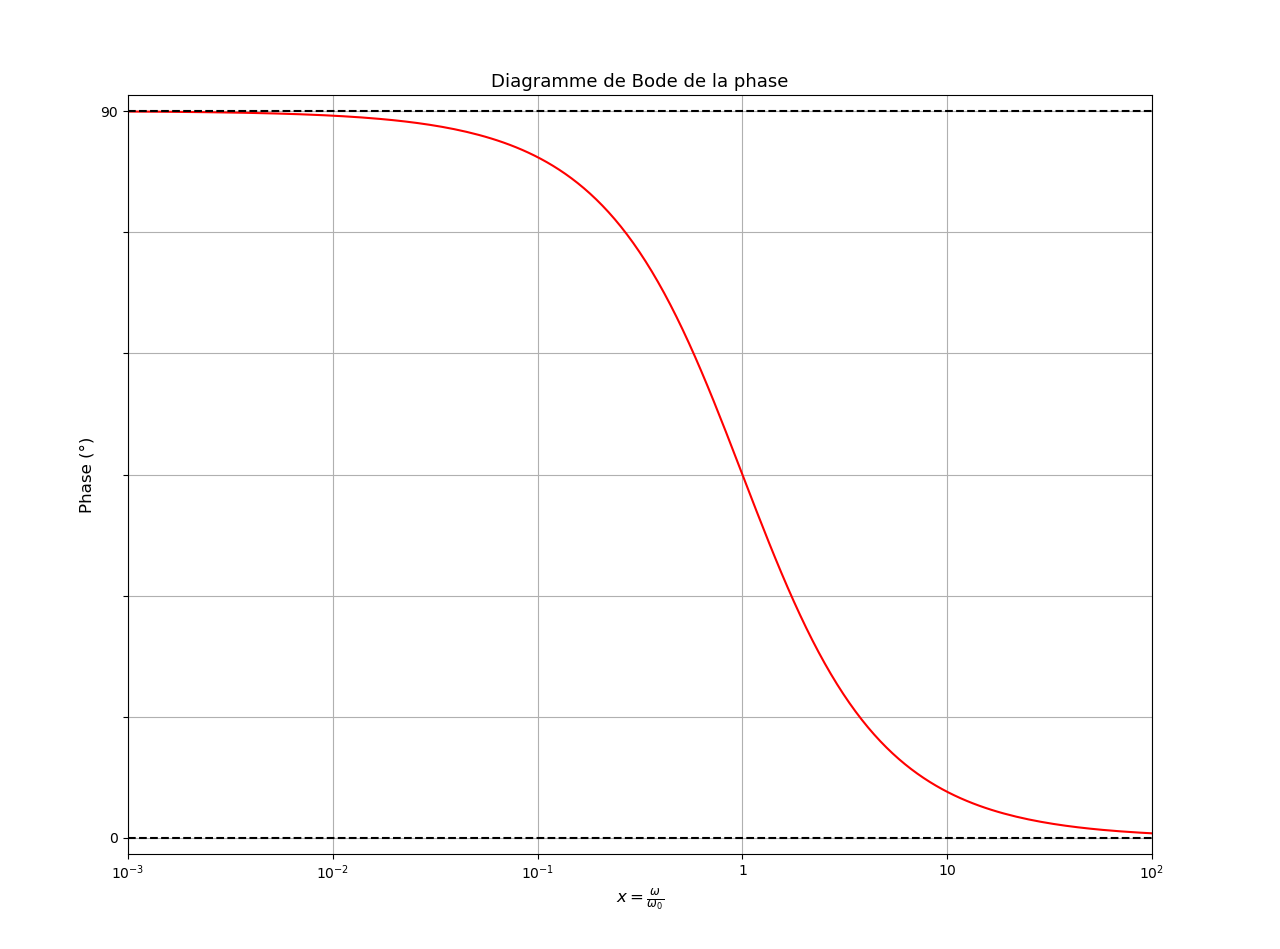
La différence de phase entre vs(t) et ve(t) est l'argument de la fonction de transfert.

Filtre passif

Filtre passif

Posté par
Physical111re : Filtre passif 30-03-23 à 14:56

Bonjour :
Pourquoi ve=vs/2 je ne comprends pas personnellement je trouve Ve=2\sqrt{2}V_s
Car :
T(\omega)=\dfrac{V_s}{V_e}=\dfrac{T_0}{\sqrt 2}
•x=\left(\dfrac{\omega}{\omega_0} \right)
Avec \omega_0=\dfrac{R}{2L}
Et =10Hz
Donc x=\dfrac{10}{10^3}=10^{-2} (sans unité)
Merci

Posté par
Physical111re : Filtre passif 30-03-23 à 16:12

On a |T(j)|=\dfrac{1}{2}\dfrac{1}{\sqrt{1+\dfrac{1}{x²}}}=\dfrac{Vs_m}{Ve_m}
Donc Vsm=\dfrac{1}{2}\dfrac{1}{\sqrt{1+\dfrac{1}{x²}}}Ve_m
Avec Vem=0,5 V (car Ve(t)=Vemcos(t)
Et x=10-2
A.N:Vs_m=\dfrac{1}{2}\dfrac{1}{\sqrt{1+\dfrac{1}{10^{-4}}}}*0,5=0,0025=2,5*10^{-3}V=2,5mV
•ah oui je comprends c'est bien Vs=1/2 Ve
Car GdB=-6dB(pour un filtre passe haut )
Gdb=20log(T0)=
20log(1/2)
T0=1/2=Vs/Ve
•pour la phase
On a =arg(T(j)=arg(1/2)-arg(1-j/x)=-arg(1-j/x)
*En basse fréquence (x<<1=> 1/x>>1)
=-arg(-1/x)=/2
*En haute fréquence (x>>1 => 1/x<<1)
=-arg(1)=0
Mais je ne comprends pas comment trouver la phase de Vsm
Et la pulsation de Vs(t) est 0=?=103Hz
Merci beaucoup

Posté par
vanoisere : Filtre passif 30-03-23 à 16:40

Cela n'est pas toujours répété dans chaque énoncé mais l'étude des filtres est supposé effectuée en régime sinusoïdal forcé : chaque tension, chaque intensité est une fonction sinusoïdale du temps ayant la pulsation imposée par le générateur.
Une pulsation se mesure en rad/s.
L'argument que tu as obtenu représente le déphsage entre vs(t) et ve(t) :
=phase(Vs(t))-phase(ve(t))

PS : je pense que tu connais l'essentiel de ce document (partie I seule utile ici) mais une piqûre de rappel sur certain points te sera peut-être utile :

Posté par
Physical111re : Filtre passif 30-03-23 à 18:50

Bonjour
Merci pour ce pdf complet
Est ce qu'il y a s'il vous plaît des erreurs dans mes raisonnements ?
On a
=phase(Vs(t))-phase(ve(t))
Or phase(ve(t))=0
Car Ve(t)=0,5cos(10t+0)
Donc =phase(Vs(t))
En haut fréquence la phase est nulle
Donc =phase(Vs(t))=?=0

Posté par
vanoisere : Filtre passif 30-03-23 à 22:00

La question porte sur l'expression de vs(t) si =10rad/s.

Posté par
Physical111re : Filtre passif 30-03-23 à 22:54

Bonjour
On a Vs=1/2 Ve et Ve(t)=0.5cos(10t)
Donc Vs(t)=1/4cos(10t)
Merci

Posté par
vanoisere : Filtre passif 30-03-23 à 23:06

Non : si =10rad/s , x=10-2 : il te faut donc calculer le module et l'argument de la fonction de transfert mais il me semble que tu as déjà fait le calcul...

Posté par
Physical111re : Filtre passif 30-03-23 à 23:15

Bonjour
Je récapitule :
On a |T(j\omega)|
=\dfrac{1}{2}\dfrac{1}{\sqrt{1+\dfrac{1}{x²}}}=\dfrac{Vs_m}{Ve_m}
Donc V_{sm}=\dfrac{1}{2}\dfrac{1}{\sqrt{1+\dfrac{1}{x²}}}Ve_m
Avec Vem=0,5 V (car Ve(t)=Vemcos(t)
Et x=10-2
A.N:Vs_m=\dfrac{1}{2}\dfrac{1}{\sqrt{1+\dfrac{1}{10^{-4}}}}*0,5=0,0025=2,5*10^{-3}V=2,5mV
•pour la phase
On a =arg(T(j)=arg(1/2)-arg(1-j/x)=-arg(1-j/x)
*En basse fréquence (x<<1=> 1/x>>1)
=-arg(-1/x)=/2
*En haute fréquence (x>>1 => 1/x<<1)
=-arg(1)=0
Mais je ne comprends pas comment trouver la phase de Vsm
Et la pulsation de Vs(t) est 0=?=103Hz

Posté par
vanoisere : Filtre passif 31-03-23 à 11:40

Citation :
Et la pulsation de Vs(t) est 0=?=103Hz

Je t'ai déjà répondu : premier paragraphe de mon message du  30-03-23 à 16:40 et cela est développé dans le premier paragraphe du document que je t'ai indiqué.
Citation :
Mais je ne comprends pas comment trouver la phase de Vsm

Ta phrase n'a pas de sens : on peut définir la phase d'une tension instantanée sinusoïdale, pas la phase d'une valeur maximale (amplitude). La tension de sortie s'écrit sous la forme :
vs(t)=Vsm.cos(.t+). La phase de vs(t) est (.t+).
est la phase initiale de vs(t). C'est aussi le déphasage de vs(t) par rapport à ve(t) puisque la phase initiale de ve(t) a été choisi arbitrairement nulle.

Posté par
Physical111re : Filtre passif 31-03-23 à 14:21

Bonjour
Donc Vs(t)=2,5*10-3cos(10-2t)
=2*f

Posté par
vanoisere : Filtre passif 31-03-23 à 15:27

Tu n'as toujours pas compris : tu confonds la pulsation et la valeur de x et tu ne tiens pas compte du déphasage introduit par le filtre entre vs(t) et ve(t).

Posté par
Physical111re : Filtre passif 31-03-23 à 22:33

Bonjour
Vs(t) et Ve(t) on même pulsation =10rad/s
Et la phase de Vs est /2
Et Vsmax=2,5*10-3V
Merci

Posté par
Physical111re : Filtre passif 01-04-23 à 18:19

Bonjour
Donc Vs(t)=2,5*10-3cos(10t+/2)
Merci beaucoup

Posté par
vanoisere : Filtre passif 01-04-23 à 18:24

Parfait !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !