Niveau maths sup

Filtre passe bande

Posté par cebora 02-06-25 à 17:16

Bonjour, voici l'énoncé :

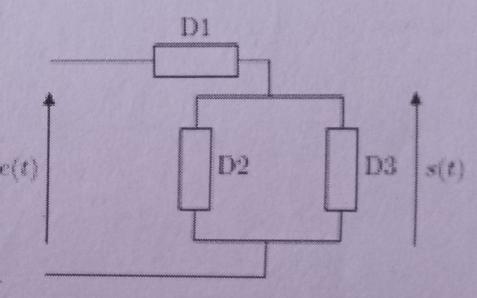
On étudie le circuit ci-dessus comportant une résistance R, une bobine idéale L, et un condensateur C.
À basse et à haute fréquences s(t) = 0. Pour un signal sinusoïdal de fréquence f_0 = 1200 Hz, on observe une résonance.
1) Par une étude qualitative, déterminer la position des composants. (1 dipôle en série et 2 dipôles en parallèle, s(t) est mesurée aux bornes du dipôle 3)
2) Faire un calcul de la fonction de transfert.
3) Calculer le produit LC.
En continu sous une tension de 10 V on relève I = 5 mA.
4) Calculer R.
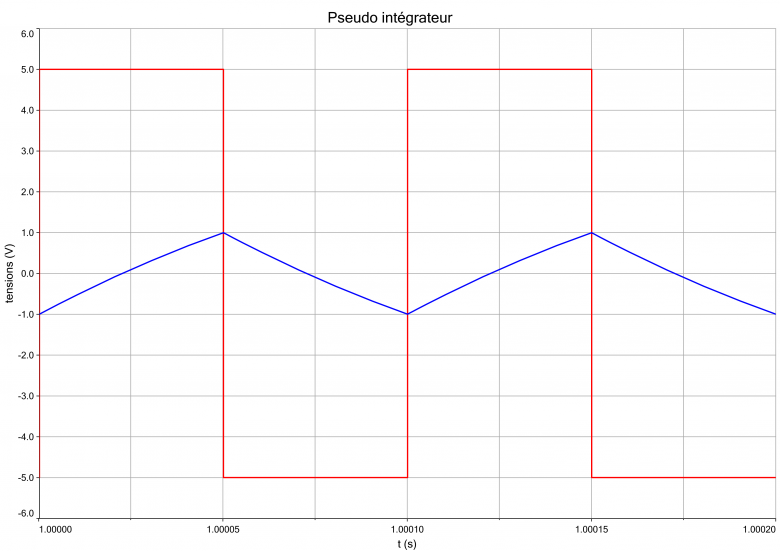
Avec une entrée créneau de fréquence 100 Hz de valeur moyenne nulle et d'amplitude 5 V, on relève une tension triangulaire d'amplitude 1 V.
5) Expliquer et calculer L et C.
6) Dans quel domaine de fréquence le circuit est-il dérivateur ?

Ce que j'ai fait :
1) Le dipôle en série est la résistance et les deux autres sont la bobine et le condensateur, c'est un passe-bande

2) $\underline{H}=\dfrac{1}{1+jQ\left(\dfrac{\omega}{\omega_{o}}-\dfrac{\omega_{o}}{\omega}\right)} \quad avec\quad LC\omega_{o}^{2}=1\quad et\quad Q=RC\omega_{o}=\dfrac{R}{L\omega_{o}}$

3) w₀ = 1/(LC) donc f₀ est donnée, on a le résultat

4) E = RI, E et I sont données donc on a R

J'ai plus de mal avec les questions 5 et 6, si quelqu'un peut vérifier mes réponses et m'aider pour les questions suivantes, merci !

Posté par re : Filtre passe bande 02-06-25 à 17:30

Bonjour
Il serait bon de fournir un schéma et d'expliquer qualitativement le rôle de (L//C) : rôle d'un "circuit bouchon" peut-être...
Comment justifies-tu ton calcul en 4) ?
Pour 5 et 6 : comment se comporte un passe bande aux fréquences très inférieures à la fréquence propre ? Comment se comporte un passe bande aux fréquences très supérieures à la fréquence propre ? (les réponses peuvent s'obtenir en simplifiant la fonction de transfert dans ces deux cas).

Posté par re : Filtre passe bande 02-06-25 à 18:15

Merci pour la réponse,
L et C en parallèle permet d'avoir le signal de sortie nul en haute et basse fréquence

Pour la 4, comme on est en régime continu, $\omega$ = 0
La bobine se comporte comme un fil et le condensateur comme un interrupteur ouvert, donc par loi des mailles , E = RI

Pour 5 et 6, en basses fréquences :
$\underline{H} \sim \dfrac{H_0}{-jQ\left(\dfrac{\omega_0}{\omega}\right)} \sim \dfrac{H_0jx}{Q}$ -> dérivateur

et en hautes fréquences : $\underline{H} \sim \dfrac{H_0}{jQ\left(\dfrac{\omega}{\omega_0}\right)} \sim \dfrac{H_0}{jxQ}$ -> intégrateur d'où la sortie triangulaire

Je ne vois pas le rapport avec le calcul de L et C

Posté par re : Filtre passe bande 02-06-25 à 18:16

et voici le circuit

Filtre passe bande

Posté par re : Filtre passe bande 02-06-25 à 21:10

Bien vu dans l'ensemble. Erreur sans doute de copie : comme tu l'as montré, le comportement en pseudo intégrateur s'obtient à fréquence grande devant la fréquence propre : 10kHz peut-être plutôt que 100Hz ???

Dans ce cas particulier, la relation que tu as écrite transposée aux valeurs instantanée devient :

$v_{s(t)}=\frac{1}{RC}\cdot\intop v_{e(t)}.dt$

ou :

$v_{e(t)}=R.C\cdot\frac{dv_{s(t)}}{dt}$

Sur une demie période où la tension d'entrée est une constante positive V_em=5V, la tension de sortie est fonction affine de t : vs(t) passe de la valeur zéro à la valeur maximale V_sm=1V en un quart de période (fais un schéma si cela ne te parait pas évident) :

$\frac{dv_{s(t)}}{dt}=\frac{V_{sm}}{T/4}=4f.V_{sm}$

$V_{em}=4f.R.C.V_{sm}$

Je te laisse terminer...