Niveau licence

Filtre passe-bande

Posté par
Pikimidb 26-11-17 à 13:09

Bonjour,
Je bloque sur une question par rapport au calcul d'une fréquence d'un passe-bande.
(c'est la suite de mon ancien exercice, je recopie l'énoncé)
Après avoir démontré que la fonction de transfert est égale à $H (jw) = A_0.\frac{1}{1+j\frac{w}{w_2}}.\frac{j\frac{w}{w_1}}{1+j\frac{w}{w_1}}$ avec $A_0 = -\frac{R2}{R1} // w_1 = \frac{1}{R1C1}//w_2 = \frac{1}{R2C2}$ , on nous demande de déterminer la fréquence f0 pour laquelle le gain est maximum.
En fait, je ne comprends pas faut-il partir du principe que le gain maximum est de 1 ?
Ou bien plutôt dériver l'expression du gain, et chercher ensuite où elle s'annule ?
Car, dans les deux cas, je trouve des résultats différents (dans le 1er cas je tombe sur une équation du 2nd degrés à résoudre et dans le 2ème cas, je trouve f0 = 1591,58 Hz environ).

Les données numériques sont les suivantes : R1 = 1kOhms, R2 = 10kOhms, C1 = 100nF, C2 = 10nF.

Merci d'avance pour l'aide apportée !

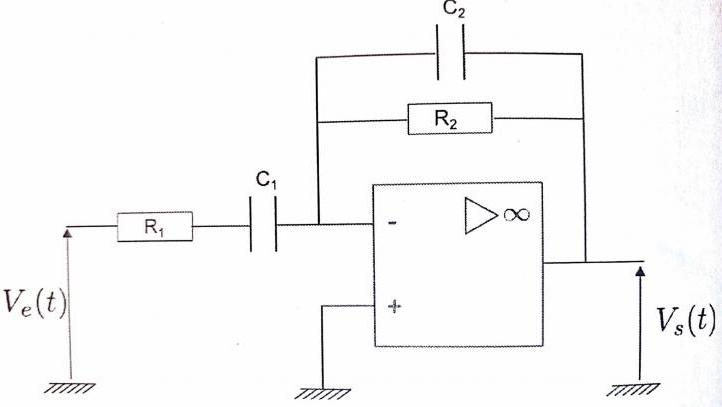
Filtre passe-bande

Posté par re : Filtre passe-bande 26-11-17 à 14:50

L'application numérique conduit à R1C1=R2C2 donc :

$\omega_{1}=\omega_{2}=\omega_{0}=10^{4}rad/s$

D'où une fréquence propre :

$f_{0}=1591Hz$

Je suis donc d'accord avec toi !

La fonction de transfert peut alors se simplifier :

$\underline{H}=\frac{1}{\left(1+j\frac{\omega}{\omega_{0}}\right)\left(1+\frac{\omega_{0}}{j\omega}\right)}=\frac{1}{2+j\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$

$\underline{H}=\frac{\frac{1}{2}}{1+j\frac{1}{2}\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$

Tu trouves la fonction de transfert classique d'un passe bas de pulsation propre wo et de facteur de qualité Q=1/2. La valeur maximale du module de H est donc 1/2. Je te rappelle l'expression générale :

$\underline{H}=\frac{A_{0}}{1+jQ\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$

Posté par re : Filtre passe-bande 26-11-17 à 15:04

J'ai oublié de prendre en compte Ao. Je rectifie

$\underline{H}=\frac{A_{0}}{\left(1+j\frac{\omega}{\omega_{0}}\right)\left(1+\frac{\omega_{0}}{j\omega}\right)}=\frac{A_{0}}{2+j\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$

$\underline{H}=\frac{\frac{A_{0}}{2}}{1+j\frac{1}{2}\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$

Tu trouves la fonction de transfert classique d'un passe bas de pulsation propre wo et de facteur de qualité Q=1/2. La valeur maximale du module de H est donc Ao/2. Je te rappelle l'expression générale :

$\underline{H}=\frac{H_{max}}{1+jQ\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)}$

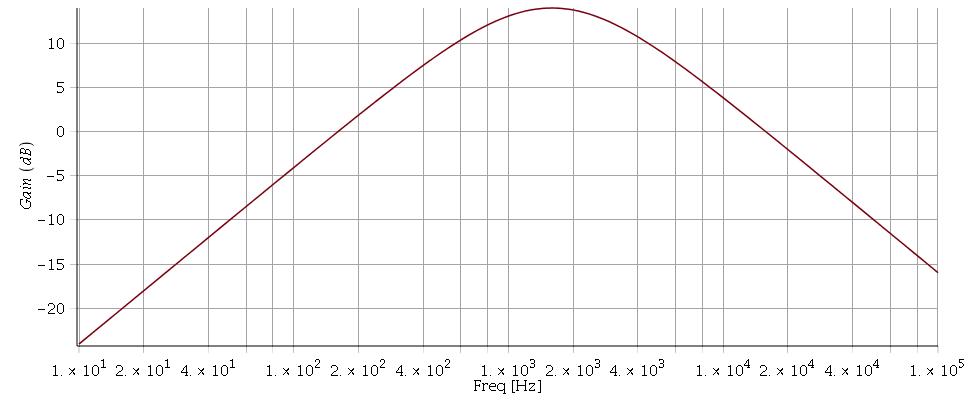
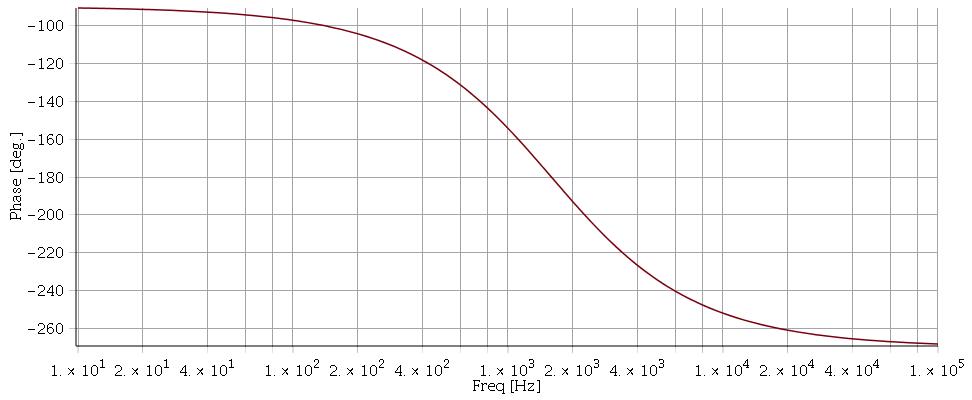
Posté par re : Filtre passe-bande 26-11-17 à 15:07

Décidément : il s'agit bien sûr d'un filtre passe-bande

Posté par re : Filtre passe-bande 26-11-17 à 15:28

Pour t'aider un peu : voici une simulation du diagramme de Bode. Attention pour la phase : le filtre est à la fois passe-bande et inverseur : d'où le décalage de 180° par rapport au passe-bande non inverseur.

Filtre passe-bande

Posté par re : Filtre passe-bande 26-11-17 à 15:59

Merci beaucoup !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Filtre passe-bande

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique