Inscription / Connexion Nouveau Sujet
filtre LCL
Bonsoir,
Je n'arrive pas à faire un exercice :
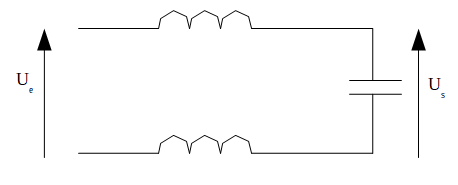
Soit un circuit L, C, L série avec ue (barre) la tension entre les deux bouts de ce filtre et us (barre) la tension aux bornes du condensateur.
On me demande d'exprimer la fonction de transfert du filtre en fonction de f et de fo, fréquence propre que l'on exprimera en fonction de L et C et que l'on calculera numériquement.
J'ai utilisé le pont diviseur de tension puis j'ai ainsi trouvé :
ce qui me paraît peu cohérent.....
Merci d'avance pour votre aide !
Bonjour
Il faudrait le schéma du filtre pour juger de la validité de ta fonction de transfert. Si celle-ci est correcte, tu n'as pas commis d'erreur dans la simplification...
C'est bien cela !
On pose souvent :
où et
désignent respectivement la pulsation propre et la fréquence propre. On obtient alors :
Du coup j'ai trouvé que le gain était égal à la fonction de transfert. Est-ce que c'est bien cela ?
Et que en f --> 0 on avait G(0)=1 et en f -->  on avait G(
on avait G( )=0. Est-ce que c'est juste ?
)=0. Est-ce que c'est juste ?
Pour l'argument je trouve  =0 car il n'y pas de partie imaginaire mais ça me semble étrange, je n'ai jamais rencontré un cas pareil
=0 car il n'y pas de partie imaginaire mais ça me semble étrange, je n'ai jamais rencontré un cas pareil
On nous demande ensuite de tenir compte de la résistance interne de chaque bobine notée r.
Déterminer l'expression de la nouvelle fonction de transfert :
J'ai réussi à mettre ma fonction de transfert sous cette forme avec : et
Après on nous demande de calculer le gain mais j'ai à nouveau un problème car je ne sais pas ce qui est la partie imaginaire dans la fonction de transfert vu qu'on a deux fois j.... A moins qu'on modifie la fonction de transfert obtenue mais je trouverais ça un peu idiot...
Merci d'avance !
Pour simplifier l'écriture, je pose :
Partie réelle et partie imaginaire apparaissent clairement, non ?
Oui effectivement mais je trouvais ça idiot d'avoir écrit la fonction de transfert sous la forme demandée si ensuite on la "modifiait".
Du coup je trouve
Ensuite on nous dit :
H(f) admet un maximum pour . Exprimer Hmax en fonction de Q et tracer l'allure du gain en fonction de f. Commenter en comparant par rapport à la courbe obtenue précédemment.
J'ai obtenu :
Du coup pour f 0 on a G(w)
0 on a G(w) 1
1
f
 on a G(w)
on a G(w)  0
0
Du coup j'obtiens la même courbe que pour la fonction de transfert précédente (cf message de 9h15 à 9h37 de hier (je ne crois pas que tu les aies vu Vanoise)) ce qui signifie que la résistance interne de chaque bobine est négligeable dans la fonction de transfert et n'a pas d'influence sur le rôle du filtre.
Est-ce que c'est juste ?
Bonsoir
Tu as écris de bonnes choses mais je crois qu'il y a ici un malentendu sur les notations. Je vais essayer de remettre cela au clair.
L'usage en électricité est de souligner les grandeurs complexes associées aux grandeurs physiques. La fonction de transfert complexe est le plus souvent notée H ou H(j ) ou H(jf)
) ou H(jf)
Le module de cette fonction de transfert complexe est le plus souvent noté H ou H( ) ou H(f). Cependant, comme ce module est le rapport des amplitudes Vsmax/Vemax, on l'appelle parfois gain en tension et on le note alors G ou G(
) ou H(f). Cependant, comme ce module est le rapport des amplitudes Vsmax/Vemax, on l'appelle parfois gain en tension et on le note alors G ou G( ) ou G(f) mais attention : ne pas confondre avec le gain en décibels !
) ou G(f) mais attention : ne pas confondre avec le gain en décibels !
Bref : tout cela pour dire que ce que ton énoncé appelle Hmax désigne le maximum de ce que l'énoncé appelle H(f) et que toi tu appelles G( ).
).
Tu es donc amenée à étudier les variations en fonction de f du module de la fonction de transfert complexe.
A noter qu'il existe un maximum de H(f) seulement pour .
L'étude des cas limites est correcte : tu obtiens un filtre passe-bas du second ordre.
Ok merci en effet je n'avais pas compris le rapport entre Hmax et G(f). Du coup, cela signifie que mon Hmax et faux ? Si Hmax correspond au maximum de G(f) alors on a en remplaçant le f dans G(f) par
? Est-ce que le
 trouvé dans mon message de hier à 9h37 était juste aussi s'il-te-plaît ? Pour les barres sous la fonction de transfert j'avais compris mais je n'arrive pas à les faire je ne sais pas où les trouver sur le site....
trouvé dans mon message de hier à 9h37 était juste aussi s'il-te-plaît ? Pour les barres sous la fonction de transfert j'avais compris mais je n'arrive pas à les faire je ne sais pas où les trouver sur le site....
J'ai été optimiste : tu as commis une erreur dans l'expression du module de H(jf) :
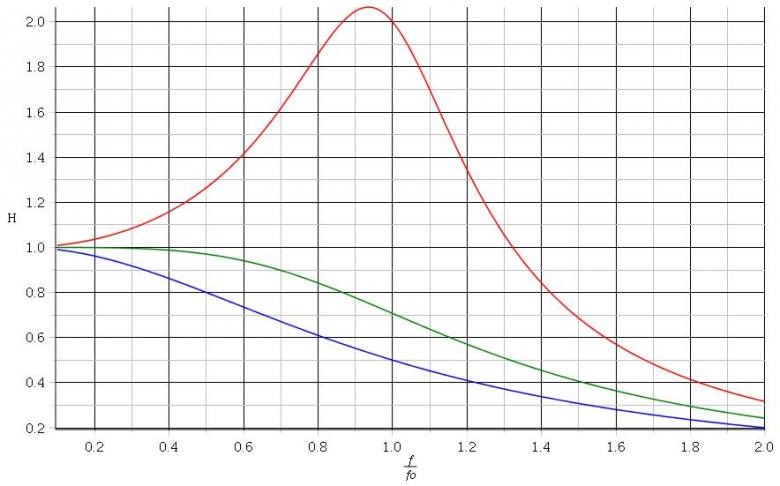
Pour t'aider voici des représentations des variation de H=G en fonction du rapport f/fo dans trois cas particuliers :
en rouge : Q=2 ; il y a bien un maximum pour une fréquence un peu inférieure à fo
en vert : Q= 2/2 : pas de maximum
2/2 : pas de maximum
en bleu : Q=0,5 : pas de maximum non plus mais décroissance de H plus rapide en fonction de la fréquence
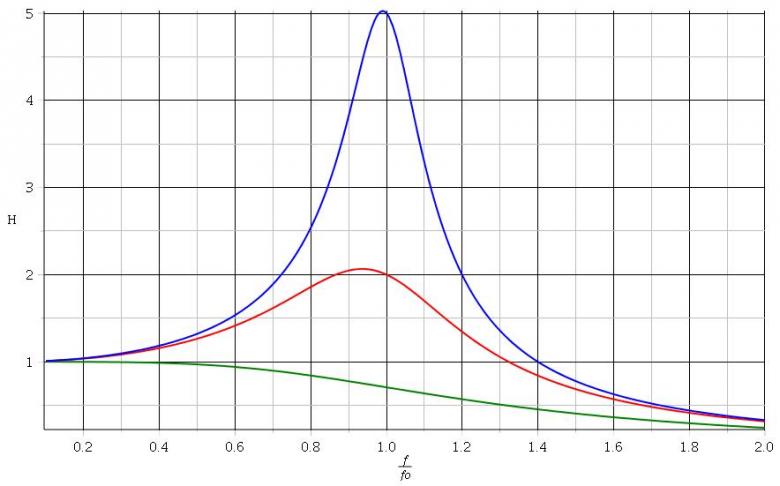
Pour bien visualiser ce qui se passe quand Q augmente :
en vert : Q= 2/2
2/2
en rouge : Q=2
en bleu : Q=5
Je te rappelle que le cas où les résistances des bobines tendent vers zéro correspond à une valeur de Q tendant vers l'infini.
J'ai essayé de recalculer Hmax et je trouve . Est-ce que c'est juste?
Pour les graphiques : plus Q est grand plus la résistance des bobines est négligeable et plus Hmax est grand. C'est ça ?
Exact sur toute la ligne ! 
On peut aussi dire que, plus Q est grand, plus la fréquence permettant d'obtenir cette valeur maximale de H est proche de la fréquence propre.
Super  Merci beaucoup !
Merci beaucoup !
Mais il me reste encore des questions 
Dans la suite, il s'agit d'une étude expérimentale qu'on devra faire en TP. J'ai trouvé comment on repérait le gain et le déphasage sur l'oscilloscope mais il y a plusieurs apescts expérimentaux que je ne vois pas comment réaliser :
-comment choisit-on une fréquence appropriée sur le GBF ?
Dans cette étude, on devra en choisir plusieurs. Comment choisit-on les "meilleurs" fréquences ?
-J'ai trouvé comment mesuré le gain mais pas comment mesurer le gain maximal sur l'oscilloscope.
-comment détermine-t'on la fréquence de coupure du montage? Là-dessus j'ai une petite idée : je pense qu'il faudra qu'on mesure G(f) (ça je sais comment faire) et qu'on divise le résultat obtenu par  2. C'est juste ?
2. C'est juste ?
Il est toujours délicat de conseiller un étudiant sur un TP sans connaître le matériel à disposition. J'imagine tout de même que ton générateur de tension sinusoïdale branché en entrée est de fréquence réglable.
Tu peux donc commencer par augmenter régulièrement la fréquence tout en vérifiant que l'amplitude de la tension d'entrée reste fixe. Le cas particulier où l'amplitude de la tension de sortie est maximale permet d'obtenir la fréquence fr et de calculer Hmax. Si tu connais les ordres de grandeurs des valeurs de L et r, un petit calcul théorique préliminaire permettrait d'obtenir un ordre de grandeur de fr, ce qui permettrait de ne pas trop "tâtonner" expérimentalement.
Ensuite, tu peux remplir un tableau de mesures en mesurant H pour différentes fréquences comprise entre 0,1fr et 2fr puis tracer la courbe représentant les variations de H en fonction de f. Elle devrait avoir l'allure de l'une de celles que je t'ai fournies.
Une fois la courbe tracée, tu peux graphiquement obtenir la fréquence de coupure en remarquant qu'elle correspond à H=Hmax/ 2.
2.