B'soir,


Il s'agit d'un exercice sur le filtre de Wien et j'ai quelque mal à résoudre l'équation différentielle à la question 4.

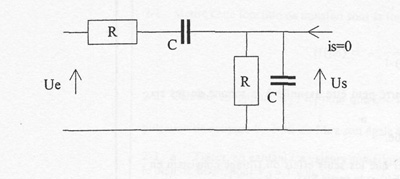
schéma du filtre de Wien:
à la fin du message
énoncé
Établir la fonction de transfert du filtre suivant, sous la forme   :

1-    Expliciter, Q et .
2-    Déduire de la fonction de transfert l'équation différentielle vérifiée par Us(t).
3-    On applique en entrée un échelon de tension du type : Ue(t<0) = 0 et Ue(t>0) = E = cte.
Donner la forme générale de la solution Us(t).
4-    Exprimer Us(t = 0+) et (dUs/dt)(t = 0+), en déduire Us(t), donner son allure .



Résolution
Q==1/3

on a l'équation différentielle suivante:



équation caractéristique:


> 0



donc la solution générale est;



il faut donc trouver les constantes, pour cela on intègre l'équation différentielle entre 0- et t->0+.



Puis il y a une histoire de termes qui s'annulent car fonctions bornées et autres raisons que je n'ai pas comprises.

Que devient l'équation différentielle et comment puis-je trouver les constantes?


Merci beaucoup =)