Quelqu'un pour une idée sur l'allure générale?

Il faudrait déjà savoir si il s'agit d'un fitre "coupe bande" comme écrit dans le titre du sujet ou bien d'un filtre "passe bande" comme écrit dans le corps de l'énoncé.

C'est juste le contraire.

De plus, s'agit d'une tension en craineau (donc juste un seul front) ou bien un signal répétitif dit "carré" ?

On peut réfléchir en imaginant le spectre en fréquence du signal d'entrée (décomposition en série de Fourier, fondamentale et harmoniques).
  
Chacune des composantes de la série de Fourier sera influencée par le filtre suivant le type du filtre et sa fréquence d'accord.
  

Desolé pour les imprecisions c'est un coupe bande et c'est un creneau périodique

Si on décompose un signal "carré" en série de Fourier, seules existent les harmoniques impairs.



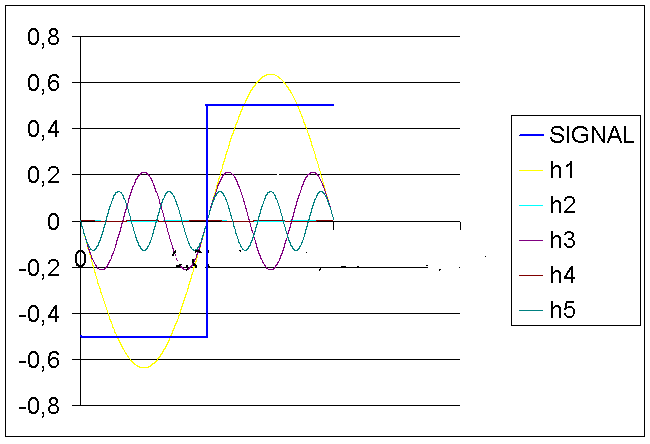
Sur le graphe, j'ai représenté une période du signal d'entrée (en bleu), ainsi que la fondamentale (en jaune) et les premiers harmoniques de la série de Fourier correspondante.

On remarque bien l'absence des harmoniques pairs.

Le signal "carré" de fréquence f est équivalent à une somme de sinusoïdes.

a) la fondamentale (en jaune) a la même fréquence que celle du signal carré.

b) les harmoniques (ici seules les impairs existent) et leur amplitude diminue avec leur rang.

Pour un signal carré variant  de 1 crète à crète, L'amplitude de la fondamentale de fréquence f est de 0,64
L'harmonique 3 a une fréquence 3f et son amplitude est 0,21
L'harmonique 5 a une fréquence 5f et son amplitude est 0,13

Voici les quelques harmoniques suivantes (non représentées sur le schéma)

L'harmonique 7 a une fréquence 7f et son amplitude est 0,091
L'harmonique 9 a une fréquence 9f et son amplitude est 0,071
L'harmonique 11 a une fréquence 11f et son amplitude est 0,057
L'harmonique 13 a une fréquence 13f et son amplitude est 0,049
...

Il faut donc voir ce que va "couper" le filtre,
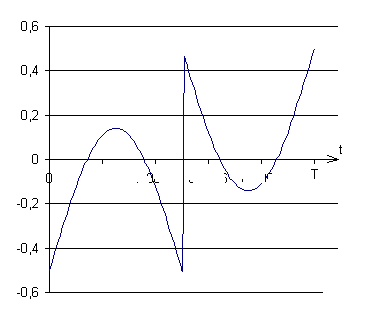
Si la fréquence du signal carré est égale ou très proche de la fréquence d'accord du filtre, le filtre va atténuer très fort la fondamentale et laisser presque intactes les harmoniques.
Le signal de sortie sera donc presque égal à celui d'entrée - la fondamentale.

Il aura une tête comme ceci :



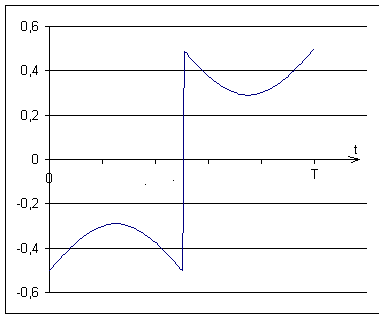
Si la fréquence d'accord du filtre est proche de la fréquence d'un des harmoniques existants (donc impair), alors cet harmonique sera trés atténué et pas les autres.
Le signal de sortie sera donc presque égal à celui d'entrée - l'harmonique concerné.

Exemple, si le filtre est centré sur l'harmonique 3, on aura un truc ainsi à la sortie :



Si le filtre est centré sur un harmonique de plus haut rang et impair, la déformation du carré sera encore moins grande.

Si le filtre est centré sur une fréquence multiple paire de le celle du carré d'entrée, alors la déformation sera quasi nulle puisque les harmoniques pairs n'existent pas dans le cas d'un signal carré.
-----
Sauf distraction.