Niveau licence

Filtre aop

Posté par
azerty4 08-03-20 à 13:01

Bonjour,

Nous avons une fonction de transfert d'un filtre avec AOP (en régime linéaire) à trouver :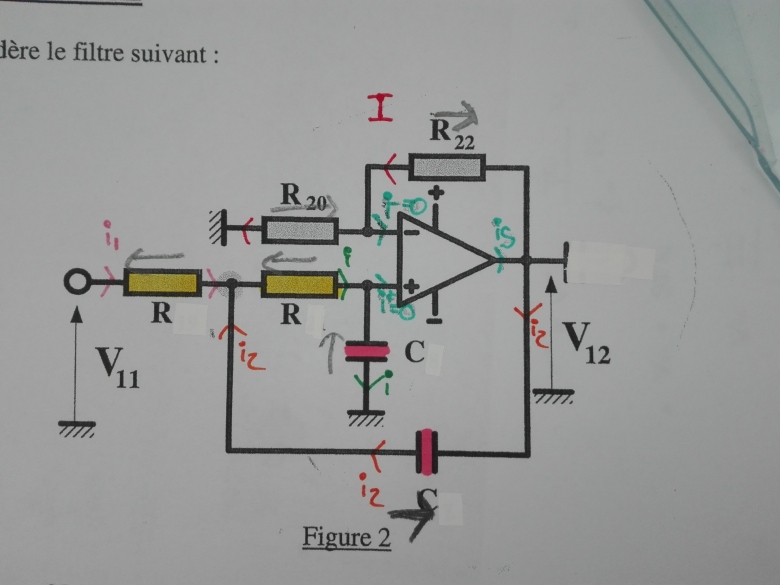

Filtre aop

Voici les équations que j'utilise :

* Loi des noeuds $i_1 + i_2 =0$
* Loi des maille : $V_{12} = I(R_{20} + R_{22})$
* Régime linéaire : $V_+ = V_-$ donc $i *\dfrac{1}{jC \omega} = I R_{20}$
* Loi des maille en passant par la source : $I(R_{20} + R_{22} ) - i_2 *\dfrac{1}{jC \omega} + i_1 R = V_{11}$
* Loi des maille en passant par la source : $I(R_{20} + R_{22} ) - i_2 *\dfrac{1}{jC \omega} + -i (R +\dfrac{1}{jC \omega} = 0$

Savez vous si ces équations de départ sont bonnes ?
On doit se ramener à un résultat sous la forme $\dfrac{V_{22}}{V_{21}} = \dfrac{T_0}{1 + 2 j z\frac{\omega}{\omega_0}-\frac{\omega^2}{\omega_0^2}}$ mais à partir de ces équation je n'y parvient pas, je suspecte donc une erreur de raisonnement dans les équation de départ ...

Merci d'avance

Bon dimanche

Posté par re : Filtre aop 08-03-20 à 13:35

Bonjour
Les lois des noeuds et des mailles sont souvent piégeantes avec ce type de circuit. Connais-tu la notion de diviseur de tension et le théorème de Millman ?

Posté par re : Filtre aop 08-03-20 à 13:48

Complément à mon message précédent un peu rapide : puisque l'ampli op fonctionne en régime linéaire, il faut procéder en trois étapes :
1° : exprimer le potentiel V_E- de l'entrée inverseuse en fonction de V₁₂ et des résistances (immédiat avec la notion de diviseur de tension) ;
2° : exprimer le potentiel de l'entrée non inverseuse V_E+ en fonction des potentiels V₁₂ et V₁₁ et des caractéristiques du circuit. C'est là que le théorème de Millman peut intervenir mais d'autres méthodes sont possibles.
3° : puisque l'ampli op fonctionne en régime linéaire : V_E+ = V_E- : en tenant compte des expressions précédentes, on obtient la fonction de transfert.

Posté par re : Filtre aop 08-03-20 à 14:41

Bonjour,
merci pour la méthode !
J'obtiens : $V_{E-} = \dfrac{R_{20}}{{R_{20}+{R_{22}}$ avec un pont diviseur
Pour Millman, j'arrive à l'écrire dans le nœud juste avant l'entrée non inverseuse (nœud grisé sur le schéma : $V_{grisé} = \dfrac{\frac{V_{11}}{R} + V_{12} j C\omega + 0 }{1/R + jC \omega + (1/R + jC \omega) }$ (sans simplification pour l'instant)

Je ne vois pas comment effectuer le théorème directement sur le nœud de l'entrée non inverseuse.

Merci pour votre aide !

Posté par re : Filtre aop 08-03-20 à 14:43

Erreur latex : *j'obtiens $V_{E-} = \dfrac{R_{20}}{R_{20}+R_{22}} . V_{12}$

Posté par re : Filtre aop 08-03-20 à 14:59

Voilà qui est beaucoup mieux et autrement plus efficace !
D'accord avec ton expression de V_E-.
En revanche, tu oublies une branche dans l'expression du potentiel du noeud N (grisé sur le schéma) :

$V_{N}=\dfrac{\frac{V_{11}}{R}+\frac{V_{E+}}{R}+jC\omega.V_{12}}{\frac{2}{R}+jC\omega}=\dfrac{V_{11}+V_{E+}+jRC\omega.V_{12}}{2+jRC\omega}$
De plus : l'ensemble RC constitue un diviseur de tension qui permet simplement d'obtenir une relation entre V_N et V_E+ .

Posté par re : Filtre aop 08-03-20 à 15:04

Petite mise au point : ton application du théorème de Millman n'est pas fausse mais simplement maladroite dans la mesure où l'étape 3 du raisonnement doit faire intervenir l'égalité entre V_E+ et V_E- .

Posté par re : Filtre aop 08-03-20 à 15:11

Merci beaucoup c'est beaucoup plus clair !
Millman évite beaucoup de calculs et limite le risque d'erreur !
Ah oui j'avais oublié de prendre en compte le potentiel VE+

J'ai donc avec un pont diviseur $V_{E+} = \dfrac{1/jC\omega}{1/jC\omega + R} = \dfrac{1}{1+jRC\omega} . V_N$

Et on obtient la fonction de transfert en quelques lignes sans faire intervenir de courant intermédiaires à supprimer avec des systèmes d'équations
Merci beaucoup pour votre aide

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Filtre aop

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique