Bonjour
Remarque préliminaire : tu as bien fait de scanner les schémas. En revanche, il faut écrire l'énoncé et tes réponses.
Pour la 1 : OK pour RC. Pour R/L : tu as sans doute étudié l'établissement d'un courant dans un circuit série R,L : on introduit là aussi une constante de temps...
Pour 2 : V_A désigne la différence de potentiels entre A et O ; V_B la différence de potentiel entre B et O. Ces deux tensions peuvent facilement s'exprimer en fonction de Ve et de caractéristiques du circuit en faisant intervenir la notion de diviseur de tension. Ensuite : V_s=V_B - V_A ; ces relations s'appliquent aux valeurs instantannées des tensions mais aussi à leurs complexes associés...
Je te laisse réfléchir à cela et proposer une solution...

Ok merci,

Donc si j'ai bien compris, V_A est la tension aux bornes de la résistance et V_B aux bornes du condensateur.
Avec le diviseur de tension :
et

C'est bien ça ?

Tu es sur la bonne voie ! Il te reste à effectuer la soustraction pour obtenir la tension de sortie complexe puis à poser :


La réponse à la question 1 devrait t'aider à trouver _o...
Je te laisse continuer !

Merci
J'ai bien trouvé la fonction de transfert demandé avec et

Ensuite question 5 :
a) Déterminer le gain en décibel H_dB correspondant.
b) Exprimer tan φ où φ est l'argument (phase) de H.

a) On a et ainsi

b) j'ai trouvé

Est-ce correct ?
Merci

OK pour ce que tu as fait sauf pour la phase. Pourrais-tu développer ton calcul de histoire de voir ce qui ne va pas ? Je ne sais pas si cela est demandé dans l'exercice mais il serait intéressant de tracer l'allure de la courbe =f(x).

Effectivement, j'ai fait une erreur de signe, en corrigeant je trouve :


J'ai séparé la partie réelle et la partie imaginaire de H complexe et j'ai pu trouver tan (phi) en faisant le rapport de la partie imaginaire sur la partie réelle.
C'est bien ?

Ensuite je dois tracer le diagramme de Bode de ce filtre
Merci

D'accord cette fois :


Tu sais bien sûr que la connaissance de la tangente ne définit l'angle qu'à rad près. Il te faut donc un renseignement complémentaire pour lever l'ambiguïté. La méthode que tu as utilisée (excellente !) t'a sans doute conduit à :


Ainsi cos() a le signe de (1-x²) et sin() le signe de (-2x).
Ainsi sin() est constamment négatif. Cela permet de lever l'ambiguïté dont j'ai parlé.
Je te laisse tracer le diagramme de Bode.

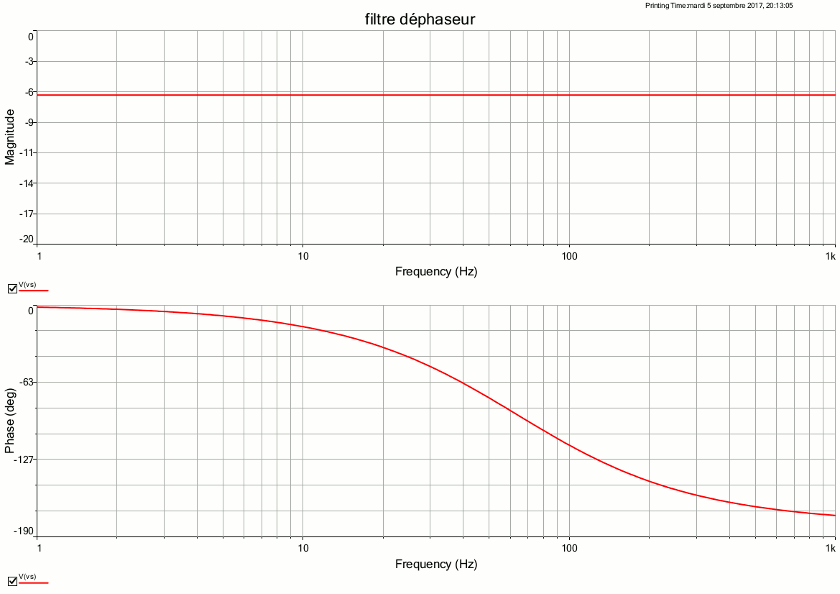
Voici, pour t'aider et "t'auto-corriger" , une simulation obtenue à partir des valeurs numériques que tu as fournies. En haut : le diagramme de Bode du gain (axe vertical gradué en dB), en bas celui de la phase (en degrés). Bien sûr : tout décalage d'un multiple de 360° est a priori recevable pour ce dernier.

D'accord merci beaucoup, je regarderai ça demain

a)

Vs/Ve = (1-jwRC)/(2.(1+jwRC))

|Vs/Ve| = 1/2
G = 20.log(1/2) = -20 * log(2) = - 6 dB

Phi = arctg(-wRC) - arctg(wRC)
Phi = - 2.arctg(wRC)

Et ceci sans aucune ambiguïté et sans devoir séparément passer par sin(Phi) et cos(Phi)
-----

Rappel :

Si z = a + ib avec a > 0, alors arg(z) = arctg(b/a) (mod 2Pi)

Si z = a + ib avec a < 0, alors arg(z) = arctg(b/a) + Pi (mod 2Pi)

Sauf distraction.  

Effectivement, il suffit d'écrire :



puisque l'argument d'un quotient est la différence des arguments et que l'opposé de l'argument d'un complexe est égal à l'argument du conjugué de ce complexe.


C'est effectivement plus simple que la méthode précédente sous réserve bien sûr que nico10310 ait une bonne maîtrise des fonctions trigonométriques inverses.
Merci JP !

Oui ok, merci à vous
J'ai une dernière question : Proposer un exemple d'utilisation d'un tel filtre.

Je pense que ce filtre permet de déphaser les signaux tout en gardant la même amplitude.

C'est effectivement un filtre déphaseur mais attention : par rapport à l'entrée, l'amplitude de la tension de sortie est divisée par deux  mais cette atténuation est bien indépendante de la fréquence ! Tu verras plus tard des filtres  déphaseurs actifs qui eux, conservent l'amplitude du signal d'entrée.

D'accord merci vanoise

Si ce n'est pas trop indiscret, qu'est ce que vous avez fait comme études ?