Inscription / Connexion Nouveau Sujet
Fil fini et champ électrostatique.
Bonjour, je bloque sur les dernières questions de cet exo.
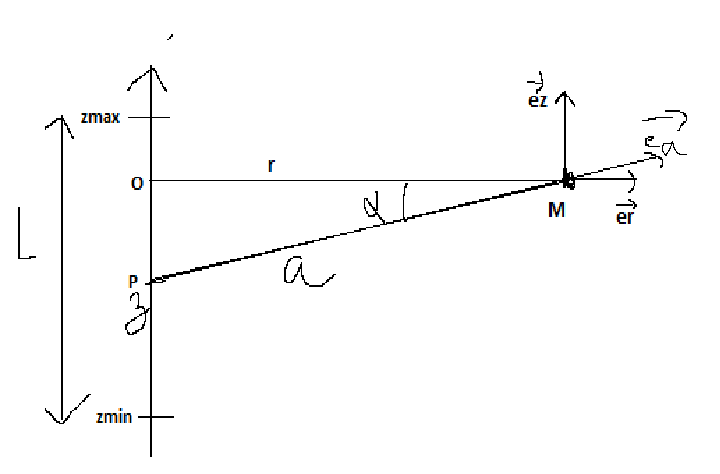
On considère un fil isolant fin, de longueur totale L = Zmin − Zmax sur lequel est répartie de manière homogène une charge totale Q. On s'intéresse au champ électrique en un point M quelconque de l'espace, et situé à une distance r du fil.
L'axe Oz est confondu avec l'axe du fil. On note par le vecteur unitaire de l'axe Oz. L'origine de l'axe z est prise au point O, point qui est la projection du point M sur l'axe Oz. Un point quelconque P du fil est repéré par sa coordonnée z. Les extrémités du fil sont les points A1 et A2 , repérées par leurs coordonnées z1 et z2.
est le vecteur unitaire porté par le vecteur
.
On appelle dans la suite :
— l'angle entre
et
, où P est un point quelconque du fil ;
— la distance entre P et M ;
— et
sont les angles qui repèrent les positions des points extrêmes du fil.
1)faire un schéma:
Le schéma paint....
2)donner la formule de la densité linéique et donner les plans de sym
Il y a un plan de sym: (M,,
)
3)Etudier les invariances
Invariance par rotation, donc le champ dépend uniquement de r et de z
4)donner , créé en M par un élément du fil de longueur
centré sur le pt P. On exprimera d'abord
en fonction de
,
, et
et des
vecteurs et
. Donner ensuite la relation entre
,
et
et celle entre
,
et
. Quelle est l'expression de
en fonction de
? Ayant fait ce changement de variable, réécrire l'expression de
en fonction de
,
,
et les vecteurs unitaires.
je pose k=
pour la relation entre ,
et
et celle entre
,
et
, je commence à bloquer.
Je trouve et
Je trouve donc (en assemblant les deux relations ou en regardant sur le schéma): , donc si je veux avoir du
et
ca me ferait aller dans du arcsin et là je commence à galérer. Enfin je pense surtout que je ne comprend pas vraiment comment trouver une variation infinitésimale à partir de ça....
5)En déduire l'expression du champ électrostatique créé par le fil en M en fonction de
,
,
et des vecteurs unitaires
et
.
Ici, j'imagine qu'en intégrant entre et
ça passe.
6). Montrer qu'on arrive au même résultat pour en écrivant le champ vectoriel élémentaire
uniquement en fonction de la variable , de la distance
et de
.
Celle là, je n'ai pas encore essayé, mais je pense qu'avec Pythagore pour enlever le du dénominateur, ça se retrouve relativement facilement (sauf peut être pour les intégrales qui risquent d'être un peu compliquées.)
Voilà! J'espère qu'il n'y a pas de coquilles dans le texte et merci d'avance pour votre aide !
Bonsoir
Remarque préliminaire concernant ton schéma ; pour ne pas te tromper de signe, tu as tout intérêt à choisir z et 
positifs sur la figure ; cela ne t'empêchera pas ensuite de raisonner en mesures algébriques.
Ici, il te faut exprimer le vecteur champ élémentaire en fonction de la seule variable de position. Il faut donc remplacer a2 par son expression en fonction de r et . De plus, puisque z=r.tan(), la différentielle s'écrit :
Cela devrait débloquer la situation...
Annuler
connectez vous