Inscription / Connexion Nouveau Sujet
Fibres Optiques
bonjour
je bloque sur certaines questions de cet exercice:
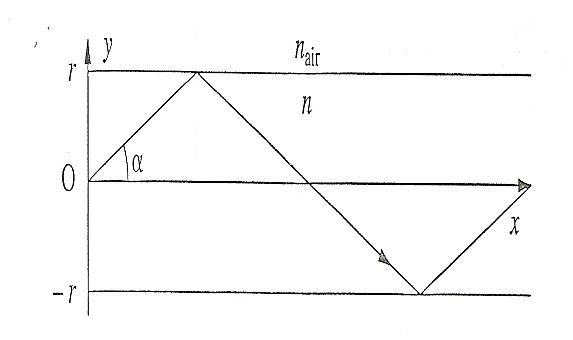
Soit un rayon lumineux partant de la source en O en faisant un angle avec l'axe de la fibre. On connait r=25 micromètre, n=1.500
1) quel est l'expression de l'angle d'incidence du rayon avec la paroi de la fibre? je pense qu'il s'agit de sin
=r/hyp
2)déterminer à l'aide de la loi de réfraction, la plus grande valeur 0 de (entre 0 et 
/2) telle qu'il n'y ait pas de rayon réfracté si 0
0. On parle de réflexion totale: le rayon ne sort jamais de la fibre
Je ne comprend pas cette question. Si la réflexion est totale, ça veut dire que i2=0?
on doit appliquer nsin=n2sini2 et trouver mais pour quelle valeur de i2 et de n2?
Pour la 1), on te demande l'angle entre le rayon et la normale au dioptre air/fibre. C'est donc '=/2-.
Pour la 2), il faut comprendre que pour un indice n1>n2, comme ici (1.5>1), il existe un angle de réfraction limite, au dessus duquel le rayon n'est plus réfracté, mais juste réfléchi.
Le rayon n'est plus réfracté si pour r l'angle de refraction, on a r>/2.
Donc, comme n1.sin i=n2.sin r, le cas limite sera r=/2, donc sin r=1, donc i(lim)=arcsin(n2/n1). Ici on a donc i(lim)='.
Voila voila !
Annuler
connectez vous