Inscription / Connexion Nouveau Sujet
Fibre optique
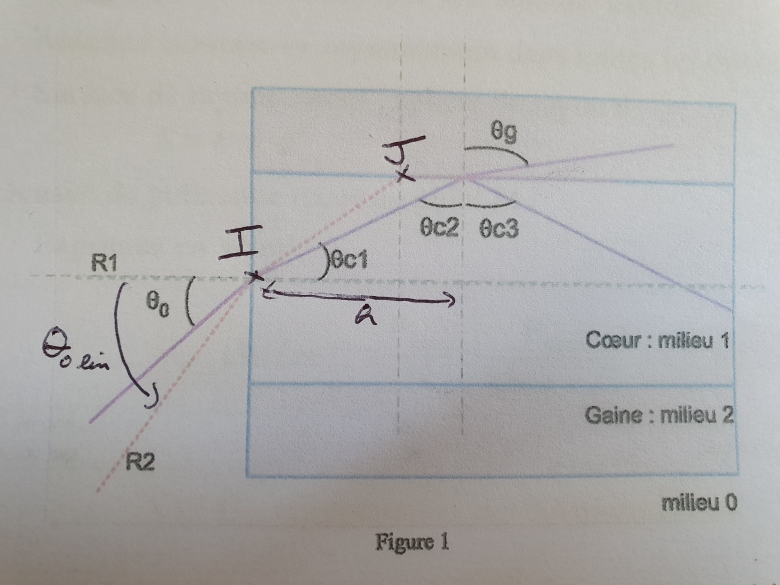
Bonjour, J'ai la figure ci-dessous.
Avec R2 rayon qui est à la limite de la réflexion totale.
Question 1) : Donner l'expression du temps T1 mis par le rayon R1 pour traverser la fibre, en fonction de L (longueur de la fibre), c (vitesse de la lumière dans le vide), et n1 (indice du cœur).
Pour cette question j'ai fais :
T1 = L/v = L*n1 / c. avec v vitesse de propagation du rayon dans le vide
Question 2) : Donner l'expression du temps T2 mis par le rayon R2 pour traverser la fibre, en fonction de L (longueur de la fibre), c (vitesse de la lumière dans le vide), et n1 (indice du cœur) et n2 (indice de la gaine). Une façon simple d'exprimer LR2 est d'exprimer les formules de cos et sin de l'angle Tetac1lim.
Pour cette question, j'ai réussi à résoudre le problème mais sans exprimer l'expression avec n2.
Le rapport entre la longueur L de la fibre et le trajet d suivi par la lumière est :
Les puissances (-1/2) ont bug apparemment ...
Donc voici ce que j'ai fais, et je ne comprends pas comment on peut exprimer avec n2, alors que le rayon R2 n'est que dans n0 et n1, et n0 = 1 ....
Bonjour
Je ne suis pas sûr de bien comprendre car les formules sont peu lisibles malgré l'effort fait pour utiliser Tex.
Si je comprends bien, tu travailles dans le cas de l'angle limite. Dans ces conditions, les angles C2 et
C2 et  C3 correspondent à l'angle de réfraction limite dont le sinus s'exprime simplement en fonction des indices n1 et n2.
C3 correspondent à l'angle de réfraction limite dont le sinus s'exprime simplement en fonction des indices n1 et n2.
Je vois, donc ici dans le cas limite on a l'angle de rétraction à 90 degrés.
Mais mon calcul devrait revenir au même résultat non ?
Je vais essayer.
Merci et désolé pour Tex, j'ai dû me mélanger les pinceaux.
Je ne comprends pas pourquoi vous utilisez ces angles, sur la figure ils ne correspondent pas au rayon R2 qui est tracé.
Mais c'est justement dans ce cas limite que ces angles sont égaux à  : angle de réfraction limite. Et justement : il existe une relation très simple entre sin(
: angle de réfraction limite. Et justement : il existe une relation très simple entre sin( ), la distance réellement parcourue (IJ) et le projeté orthogonal L de cette distance sur l'axe de symétrie de la fibre. L'expression de T2 en fonction de L, de c et des indices n1 et n2 s'obtient quasiment "de tête". Rien à voir avec les longs calculs que tu as posés dans ton premier message.
), la distance réellement parcourue (IJ) et le projeté orthogonal L de cette distance sur l'axe de symétrie de la fibre. L'expression de T2 en fonction de L, de c et des indices n1 et n2 s'obtient quasiment "de tête". Rien à voir avec les longs calculs que tu as posés dans ton premier message.
Désolé mais je n'arrive pas à avoir la logique, par rapport à la figure. Pour moi l'angle n'est pas un angle de réfraction, l'onde est réfléchie dans le coeur de la fibre, donc cette angle, pour moi, correspond à un angle réfléchi.
En fait, on nous dit que le rayon R2 est à la limite de sa réflexion totale, donc cela veut dire que plus loin, il ne rentre plus dans le coeur de la fibre. Donc ici il traverse et après il est réfléchi dans le coeur de la fibre, et, d'après la figure, je ne comprends pas pourquoi on parle d'angle de réfraction, de c3 ....
Et je comprends encore moins le arcsinus que vous avez écrit 
Je viens de commencer ce chapitre donc j'ai un peu de mal à me mettre dedans.
Merci en tout cas pour vos réponses. 
Dans le cas limite étudié ici, l'angle de réflexion totale est égal à l'angle de réfraction limite. Revois au besoin ton cours sur le sujet.
Bonjour,
Je poursuis le raisonnement de Vanoise sous réserve de sa validation :
- Soit H la projection orthogonale de J sur l'axe de la fibre : on a IH/IJ =sin(lamda) = n2/n1
- si v est la vitesse de la lumière dans le coeur, alors n1= c/v soit v = c/n1
Supposons que la longueur de la fibre soit IH et que t soit le temps avec lequel le rayon parcourt IJ ;
Alors IJ = t*v d'où IH = t*v* (n2/n1) = t*c*n2/(n1**2) d'où t = IH*(n1**2)/(c*n2)
- Miantenant si la longueur de la fibre n'est pas IH mais L = k*IH, alors le temps mis par la lumière pour la parcourir sera k*t = T2 c 'est à dire L*(n1**2)/(c*n2) =T2
Cordialement
Bonjour à tous,
@Chimival : ce n'est pas la première fois que je constate ces derniers temps que tu finis par proposer des solutions en lieu et place de celui qui demande initialement de l'aide.
Sache que ce n'est pas leur rendre service et ne respecte nullement la règle de bienséance propre à nos 3  .
.
Je te demande donc de ne plus faire cela dès à présent.
Bon après-midi


