Niveau licence

fem d'un moteur a c.a

Posté par
esaali 03-12-15 à 21:09

bonsoir,
comment demontrer la relation de fem d'un moteur a c.a : E= NLrwB sin(wt)
je commence de la demontrer et je trouve cos(wt) au lieu de sin(wt)
j'ai calculer le flux qui est egale a ?=?? B.dS pour le remplacer dans la relation de Faraday e = - d? / dt et j'ai trouver E= NLrwB cos(wt) ????

merci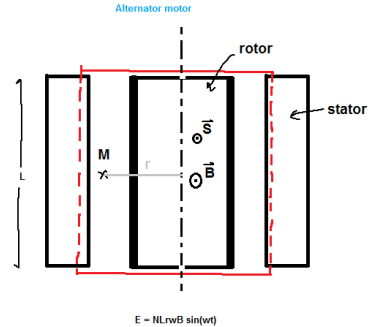

$fem d\'un moteur a c.a$

***Edit gbm : image recadrée***

Posté par re : fem d'un moteur a c.a 04-12-15 à 11:55

Bonjour,
si tu appelles l'angle entre les vecteurs B et S le flux magnétique à travers le cadre peut s'exprimer de la façon suivante :
$\begin{cases} \\ \Phi=N\overrightarrow{B}\overrightarrow{S} & \Phi=NBS\cdot\cos\left(\theta\right)\\ \\ \theta=\omega t & \Phi=NBS\cdot\cos\left(\omega t\right)\\ \\ \text{loi de Faraday :} & e=-\frac{d\Phi}{dt}\\ \\ \boxed{e=NBS\omega\cdot\sin\left(\omega t\right)} & \text{avec :\ensuremath{S=L\cdot r}} \\ \end{cases}$
avec : L = longueur de cadre ; r : largeur du cadre. Attention : la largeur du cadre est parfois notée 2r avec r : rayon ; dans ce cas, il faut poser S = 2L.r et non S = L.r

Posté par re : fem d'un moteur a c.a 05-12-15 à 15:01

merci vanoise ,
mais l'explication de flux que tu mas poser n'est pas logique , je veux utiliser la relation de flux qui égale a l'intégrale sur la surface de B fois la dérivé de la surface , comment se montre ça ?

Posté par re : fem d'un moteur a c.a 05-12-15 à 17:43

Dans ce problème, la variation de flux magnétique est uniquement due à la variation au cours du temps de l'angle entre les vecteurs B et S. Les valeurs des normes de ces vecteurs sont des constantes ici ...

Citation :
la relation de flux qui égale a l'intégrale sur la surface de B fois la dérivé de la surface , comment se montre ça ?

Tu peux traduire cette phrase en français ?

Citation :
mais l'explication de flux que tu mas poser n'est pas logique

Sans parler de la grammaire et de l'orthographe, je pense qu'il faut que tu revois sérieusement ton cours sur l'induction avant d'accuser les gens qui veulent t'aider de manquer de logique...

Posté par re : fem d'un moteur a c.a 06-12-15 à 18:49

je suis désole .
Ce ne sont pas ce que je veux dire, je ne perfectionné la langue française

Posté par re : fem d'un moteur a c.a 14-12-15 à 15:04

quelqu'un m'explique ça svp

Posté par re : fem d'un moteur a c.a 14-12-15 à 15:11

quelqu?un m?explique ça svp

***Image supprimée***

$\Phi = N.\vec{B}.\vec{S}=N.B.S.cos(\theta)$

***Edit gbm : seuls les schémas ou photos sont tolérés sur le forum, merci de faire de même que ci-dessus la prochaine fois***

Posté par re : fem d'un moteur a c.a 14-12-15 à 20:29

Bonsoir,

C'est tout simplement un appel à la notion de produit scalaire vue en première S en maths ...

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

fem d'un moteur a c.a

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique