Inscription / Connexion Nouveau Sujet
Face à face mortel entre un poisson et un pêcheur
Bonjour à tous, j?ai un exercice à faire dans l?enseignement « optique et instrumentation », dans le but de savoir déterminer l?image d?un objet à travers un dioptre plan.
Je suis un peu bloquée dès la première question parce que je vois pas trop comment je dois m?y prendre.
Voici l?énoncé:
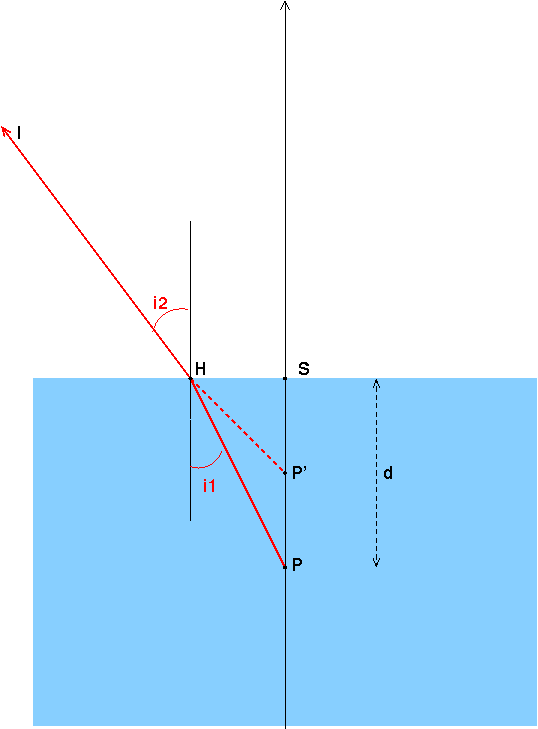
Un poisson (P) et un pêcheur (H) s?observent de part et d?autre de la surface libre d?une mare. L?oeil O du pêcheur et l??il P du poisson sont situés sur la même verticale à la distance d de la surface de l?eau.
Le schéma est joint, voici la légende :
H: position de l?homme
P: position du poisson
S: sommet du dioptre
P?: position de l?image du poisson vue par l?homme
H?: position de l?image de l?homme vue par le poisson
1) Trouver les positions des images P? et H? sur le schéma.
Personnellement je dirai que, la position de l?image de l?homme vue par le poisson est plus loin que la position de l?homme. Et que la position de l?image du poisson vue par l?homme est plus près que la position du poisson, mais je ne sais pas où les situées.
2) A quelle distance l?observateur voit il le poisson ?
3) A quelle distance le poisson voit il l?observateur ?
Je pense que c?est deux questions je pourrais y arriver quand j?aurais le schéma.
Données : d=1,2m ; neau= 1,33 .
Merci de bien vouloir m?aider. 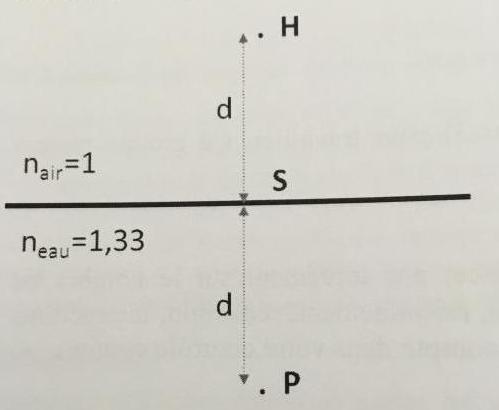
***Image recadrée***
Bonjour
J'imagine que tu as eu un cours sur le dioptre plan...
Imagine plusieurs rayons lumineux issus de P et se propageant au voisinage de la verticale en direction de l'homme. Les rayons reçus par l'il de l'observateur sembleront provenir d'un point P' qui est l'image virtuelle de P par le dioptre plan...
Essaie de faire une figure propre puis fais le calcul en supposant les rayons peu inclinés par rapport à la verticale passant par S et P...
Tu peux scanner ta figure et la poster ici...
J'imagine bien des rayons de part et d'autre mais je ne vois pas le rapport avec les points que je cherche, car ils vont partir des deux côtés
oui mais leurs prolongements passeront par un même point pour peu que ces rayons restent proches de la verticale, ce qui est le cas des rayons issus de P pénétrant dans l'il de l'observateur.
Mais ce point par lequel vont passer les rayons de part et d'autre de mon axe vertical est défini comment ?
Je considère P comme un point objet réel qui émet de la lumière dans toutes les directions.
Le rayon PS est réfracté en S sans subir de déviation (voir lois de Descartes). Donc l'image P' de P sera sur cette verticale passant par S et par P.
Je considère un second rayon PH incliné par rapport à la verticale de l'angle i1. ce rayon est diffracté en s'écartant de la verticale d'un angle i2 tel que :
sin(i2)=neau.sin(i1)
neau>1 donc : i2>i1.
Attention : pour la clarté de la figure, les angles i1 et i2 sont assez grands. En pratique, il faut les imaginer très petits de sorte que le rayon diffracté dans l'air reste peu écarté de la verticale pour pénétrer dans l'oeil de l'observateur.
Pour l'observateur, le rayon vertical et le rayon (HI) semble provenir d'un point P' situé sur la verticale passant par P. Peut-on dire que P' est l'image virtuelle de P ? Pour pouvoir répondre "oui", il faut d'abord s'assurer que tous les rayons émis par P, pourvu qu'ils soient peu inclinés par rapport à la verticale, produisent des rayons réfractés dont les prolongements passent par P'. Pour cela, il faut s'assurer que la distance d'=P'S est indépendante de la distance SH. Pour cela, il suffit d'exprimer cette distance SH en considérant les triangles rectangles (SHP) et (SHP') :
soit :
C'est maintenant qu'il faut tenir compte des angles très petits. Pour de tels angles, le rapport des tangentes est très peu différent du rapport du sinus qui est connu par la loi de Descartes :
Le poisson apparaîtra donc plus près de la surface qu'il n'est en réalité. L'observateur l'imaginera ainsi plus gros qu'il n'est en réalité.