Inscription / Connexion Nouveau Sujet
expression de problème de relativité
Bonjour,
J'ai un problème de relativité sous forme d'énoncé "vague", que je dois donc exprimer puis résoudre (niveau L2 Physique). Il s'agit d'un hors-jeu de football. J'ai fait le schéma ci dessous, qui est un schéma "vu de côté" sur un axe "x" unidimensionnel.
Obs1(fixe)______________P(fixe)__________A(vitesse V)_________D(fixe)_______x
Obs2(mobile, vitesse V)
Il faut bien comprendre que Obs2 est en mouvement au même niveau que A. P va passer la balle à "A".
Deux scénarios sont possibles : Au moment de la passe (quand P touche le ballon), A est avant D. Ou, au moment de la passe A est après D.
La question est de savoir si il est possible que Obs1 et Obs2 voient quelque chose de différent.
Ce que j'ai fait jusqu'ici c'est définir les deux évènements : "P touche la balle pour la passer à A" et
: "A dépasse D"
J'utilise l'invariant relativiste , je prend le référentiel R avec l'origine en P et les x croissants vers la droite comme sur le schéma, et pose :
et
j'ai pris "y" pour le temps comment constante arbitraire positive... on aurait pu aussi prendre "0" je pense, car on compte le temps à partir de quand P touche le ballon pour faire la passe. Ce n'est que cet instant qui compte pour le problème...
Je calcule l'invariant "Intervalle spatio-temporel" et j'obtiens : , donc
(car D positif). Donc c'est un invariant de type espace ce qui signifie qu'on ne peut pas avoir de référentiel dans lequel les évènements sont inversés. Donc il est impossible que Obs1 et Obs2 voient des scénarios différents.
Est-ce que le raisonnement est juste ? Y a-t-il plus intéressant à faire ? J'ai aussi fait les transformations de Lorentz mais je ne vois pas bien comment m'en servir pour résoudre, ou si c'est "mieux" que de passer par l'invariant.
Merci d'avance pour votre aide
Bonsoir,
Un exo très surprenant !
(en général c'est des fusees ou des trains
)
Si je comprends bien ton raisonnement, tu te places dans R (où obs1 est fixe) à la limite du hors-jeu (la passe à lieu juste au moment où A dépasse le défenseur D, donc E1 et E2 sont simultanés dans R)
Et tu fais remarquer que l'intervalle E1 et E2 est alors de genre espace ce qui est tout à fait juste.
...ce qui signifie qu'on ne peut pas avoir de référentiel dans lequel les évènements sont inversés.
Là dommage, il y a une confusion: c'est l'inverse!
Donc l'ordre chronologique de E1 et E2 dépend du référentiel
Mais tu es bien parti, je pense. Il reste à vérifier si Obs2 peut "voir" un hors-jeu
, c'est à dire que E1 est postérieur à E2 dans R2 (lié à obs2)
Cet exercice classique est tiré du manuel "Introduction à la physique moderne : relativité et physique quantique" (p. 258).
Vous n'y trouverez pas la solution mais la décomposition du problème en plusieurs étapes élémentaires pour arriver au but.
Bon travail
Bonjour krinn, oui c'est vrai que le problème est original
Oui tu as tout à fait compris mon approche, cependant j'y réfléchissais et je pense que je vais changer un tout petit peu pour prendre E1 < E2 dans R (au lieu de E1=E2), et voir si on peut donc avoir E1 = E2 (simultanés) ou E1 > E2 dans R2... car en fait E1 = E2 est un peu une situation "litigieuse", "pas claire" dans le hors jeu.
Là dommage, il y a une confusion: c'est l'inverse!
Donc l'ordre chronologique de E1 et E2 dépend du référentiel
Oui j'avais pourtant bien écrit ça dans mes notes mais je me suis trompé dans l'exercice, ça devait être à cause de la fatigue désolé, effectivement étant donné la nature "espace" de l'intervalle il existe un référentiel dans lequel E1 et E2 sont "inversés" chronologiquement.
Mais tu es bien parti, je pense. Il reste à vérifier si Obs2 peut "voir" un hors-jeu
, c'est à dire que E1 est postérieur à E2 dans R2 (lié à obs2)
D'accord donc j'imagine qu'il faut exprimer E1 et E2 dans les coordonnées de R2 avec les transformations de Lorentz... j'avoue ne pas voir ce qu'il faut faire après mais je vais essayer de le faire ce soir et je dirai ici ce que je trouve. Merci de ton aide en tout cas
Cet exercice classique est tiré du manuel "Introduction à la physique moderne : relativité et physique quantique" (p. 258).
Vous n'y trouverez pas la solution mais la décomposition du problème en plusieurs étapes élémentaires pour arriver au but.
Bon travail
Ah bon d'accord merci ça peut toujours servir !
D'accord donc j'imagine qu'il faut exprimer E1 et E2 dans les coordonnées de R2 avec les transformations de Lorentz...
oui, tu peux par ex. te placer en configuration standard (je suppose que tu l'as vue), avec E1 comme événement d'origine dans R et R' (noter R' plutot que R2 , et les coordonnees x', t' dans R' car c'est l'usage dans les formules)
donc E1(0,0) dans R et dans R'.
E2(...) dans R
E2(...) dans R'
...
...
oui, tu peux par ex. te placer en configuration standard (je suppose que tu l'as vue), avec E1 comme événement d'origine dans R et R' (noter R' plutot que R2 , et les coordonnees x', t' dans R' car c'est l'usage dans les formules)
Désolé mais je n'ai pas vu la "configuration standard" je ne sais pas ce que c'est...
donc E1(0,0) dans R et dans R'.
E2(...) dans R
E2(...) dans R'
...
...
C'était mon intention de faire ça à la base E1(0,0) dans R et dans R', mais cela voudrait dire que à l'instant t0=t'0=0, le passeur (P) et l'attaquant (A) sont dans la même position ce qui n'est pas forcément le cas... mais bon j'imagine que ça ne pose pas vraiment de problème dans la logique de la solution.
Du coup je l'ai fait, j'ai :
dans R :
dans R' :
dans R :
dans R' :
Le problème c'est qu'avec ces conditions je trouve un invariant intervalle spatio-temporel comme ceci :
Donc ce n'est plus vraiment clair le signe de cet intervalle.... enfin il est positif pour "d petit" mais il pourrait en théorie être négatif avec un "d" assez grand, donc je suis confus
Désolé mais je n'ai pas vu la "configuration standard" je ne sais pas ce que c'est...
Je pense que si, mais tu appelles ça la transformation spéciale de Lorentz (cf dessin)
A t=0 dans R, et à t'=0 dans R' , O est confondu avec O', et les axes des refs sont parallèles 2 à 2.
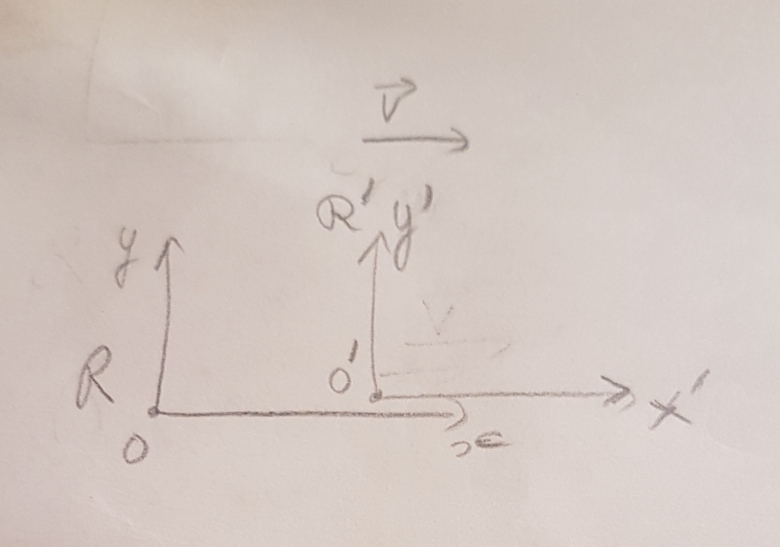
C'était mon intention de faire ça à la base E1(0,0) dans R et dans R', mais cela voudrait dire que à l'instant t0=t'0=0, le passeur (P) et l'attaquant (A) sont dans la même position
Non, ça signifie que O et O' sont confondus à t=t'=0 avec P quand il touche la balle (cad l'événement E1) , mais A n'est pas en O à t=0 dans R.
Donc :
E1(0,0) dans R
E1(0,0) dans R'
E2(d, t2) dans R (inutile de rajouter une variable y)
E2(x'2, t'2) dans R'
E2 étant l'événement "A dépasse le défenseur" (il franchit la limite du hors jeu)
On obtient alors :
x'2 = ...
t'2 =
(t2 - Vd/c2)
Donc ce n'est plus vraiment clair le signe de cet intervalle....
Il faut que l'intervalle soit négatif, donc |t2| < d/c
De plus, on veut que si t2 ≥0 dans R (pas de hors jeu) alors t'2 <0 dans R' (hors jeu) , ou l'inverse : est-ce possible?
Désolé mais je n'ai pas vu la "configuration standard" je ne sais pas ce que c'est...
Je pense que si, mais tu appelles ça la transformation spéciale de Lorentz (cf dessin)
A t=0 dans R, et à t'=0 dans R' , O est confondu avec O', et les axes des refs sont parallèles 2 à 2.
Oui c'est ce que j'ai considéré dans mes expressions de E1 et E2 dans R et R' dans mon précédent message, je pense qu'elles sont justes par rapport au dessin. Par contre en y repensant ça veut dire l'attaquant part d'a côté du passeur au même moment que le passeur touche la balle pour faire la passe... donc finalement je pense que "physiquement" ça n'a pas trop de sens de prendre les origines confondus à t=t'=0... ça se trouve je devrais rester sur ce que j'avais fait au début car physiquement c'est plus clair au niveau de la situation, du moins c'est ce que je pense
Par contre en y repensant ça veut dire l'attaquant part d'a côté du passeur au même moment que le passeur touche la balle pour faire la passe...
Non, lis la suite (post de 22:09) , nos posts seront croisés ...
Désolé pour le cross-post !
Non, ça signifie que O et O' sont confondus à t=t'=0 avec P quand il touche la balle (cad l'événement E1) , mais A n'est pas en O à t=0 dans R.
Je ne comprend pas ce point là. Le référentiel R est fixé sur le joueur "P" et Le référentiel R' est "fixé" sur le joueur "A", donc si O et O' sont confondus à t=t'=0, forcément P et A sont à la même valeur de "x" à ce moment là, c'est à dire 0....
Peut-être que tu considères que R' est centré sur la balle ? Moi je n'ai jamais considéré la balle du tout...
J'aurais sans doute dû préciser que dans l'énoncé et c'est une des rares choses qui est précisée c'est qu'on nous dit :
"Le hors-jeu peut être constaté par l'arbitre de ligne (qui va à la même vitesse que l'attaquant en mouvement), et l'arbitre de touche (qui lui est immobile par rapport aux buts).
Si maintenant on considère que l'attaquant se déplace à une vitesse relativiste, le hors-jeu reste-t-il une règle absolue ? En d'autres termes, les deux arbitres vont-ils à tous les coups constater la même chose ?"
(En fait il s'agit de l'intégralité de l'énoncé à part l'explication du hors-jeu en football)
Je ne comprend pas ce point là. Le référentiel R est fixé sur le joueur "P" et Le référentiel R' est "fixé" sur le joueur "A",
Non, l'origine de R' est O' (ce n'est pas A)
On ne peut pas prendre P et A pour se mettre en config. standard
Imagine l'arbitre de champ a côté de P au moment de la passe (donc en O a t=t'=0), et qui court derriere A a la meme vitesse que A (dans R) , c'est lui O'
Je ne comprend pas ce point là. Le référentiel R est fixé sur le joueur "P" et Le référentiel R' est "fixé" sur le joueur "A",
Non, l'origine de R' est O' (ce n'est pas A)
On ne peut pas prendre P et A pour se mettre en config. standard
Imagine l'arbitre de champ a côté de P au moment de la passe (donc en O a t=t'=0), et qui court derrière A a la meme vitesse que A (dans R) , c'est lui O'
D'accord mais donc "A" est devant "P" ET "Obs2" au moment de la passe. Donc Obs2 ne peut pas être "à côté" de A, il est à côté de P, comme ceci (à t=t'=0) :
(O de R fixé sur P, O' de R' fixé sur Obs2)
__________________P_______________A________
Obs2
Moi j'avais compris que Obs2 était au niveau de "A", car en vrai c'est comme ça qu'un arbitre de ligne se place pour voir les hors-jeu, ça n'aurait pas de sens qu'il soit au niveau du passeur. C'est pour ça que je voyais la situation plus comme ça :
__________________P_______________A________
Obs2
Mais ça se trouve cette configuration ne fonctionnerait pas bien pour le problème
D'accord, je vois pourquoi ça te gêne.
En fait ce qui est important ici, c'est que A et O' soient fixes dans R' galiléen, mais ils n'ont pas besoin d'être confondus pour pouvoir définir le même temps t'
Mais on peut se passer de la config. standard si ça te gêne.
Prenons tjs R où P est fixe en x=0 et tape à t=0 la balle pour faire sa passe (E1)
Et R' lié à A, avec l'axe Ax' confondu avec Ox
On a alors:
E1(0,0) dans R
E1( x'1, t'1) dans R'
E2(d, t2) dans R
E2(x'2, t'2) dans R'
On peut alors appliquer la transformation de Lorentz au couple d'événements E1 et E2 en écrivant:
x' = x'2-x'1= (x- Vt)
t' = t'2-t'1= (t - Vdx/c2)= (t2 - Vd/c2)
L'intervalle s2 = c2t2 - x2= c2t22- d2
On retrouve la même chose:
Il faut que l'intervalle soit négatif, donc |t2| < d/c
De plus, on veut que si t2 ≥0 dans R (pas de hors jeu) alors t'<0 dans R' (hors jeu) , ou l'inverse : est-ce possible?
On retrouve la même chose:
Il faut que l'intervalle soit négatif, donc |t2| < d/c
Je ne comprend pas pourquoi "il faut que l'intervalle soit négatif"... l'intervalle spatio-temporel a un signe de par les données du problème, je ne vois pas en quoi on pourrait dire quel devrait être son signe désolé je ne comprend pas l'idée derrière ça
De plus, on veut que si t2 ≥0 dans R (pas de hors jeu) alors
t'<0 dans R' (hors jeu) , ou l'inverse : est-ce possible?Je comprend que si
On a donc le fait que Obs2 verra un hors jeu alors que Obs1 n'en voit pas si on a :
C'est toi qui as fait remarquer, dès le début, que l'intervalle entre E1 et E2 doit être de genre espace si on veut que les arbitres ne soient pas d'accord sur le hors-jeu (cad que E1 et E2 n'ait pas le meme ordre chronologique dans R et R').
donc: |t2| < d/c et comme d/c 
10-7 s, on en deduit en fait déjà que t2 0 ( dans le cadre d'un match de foot)
On a donc le fait que Obs2 verra un hors jeu alors que Obs1 n'en voit pas si on a :
oui, ce qu'on peut écrire: t2 <
d/c avec = v/c < 1
donc ca confirme que t2
0 (limite du hors-jeu dans R)
et
t´ -d/c
et il faut discuter ce résultat.
Si maintenant on considère que l'attaquant se déplace à une vitesse relativiste, le hors-jeu reste-t-il une règle absolue ? En d'autres termes, les deux arbitres vont-ils à tous les coups constater la même chose ?"
C'est toi qui as fait remarquer, dès le début, que l'intervalle entre E1 et E2 doit être de genre espace si on veut que les arbitres ne soient pas d'accord sur le hors-jeu (cad que E1 et E2 n'ait pas le meme ordre chronologique dans R et R').
Bonjour, oui c'est vrai que j'avais calculé l'invariant dans "R" et trouvé négatif, donc et on a toujours ce même "R" dans notre configuration, donc ça fonctionne, l'invariant doit être négatif.
donc: |t2| < d/c et comme d/c
10-7 s, on en deduit en fait déjà que t2 0 ( dans le cadre d'un match de foot)
On a donc le fait que Obs2 verra un hors jeu alors que Obs1 n'en voit pas si on a :
oui, ce qu'on peut écrire: t2 <
d/c avec = v/c < 1
donc ca confirme que t2
0 (limite du hors-jeu dans R)
et
t´ -d/c
et il faut discuter ce résultat.
Si maintenant on considère que l'attaquant se déplace à une vitesse relativiste, le hors-jeu reste-t-il une règle absolue ? En d'autres termes, les deux arbitres vont-ils à tous les coups constater la même chose ?"
Pour R',
Cependant ce raisonnement ne vaut que si "d" est très très petit devant "c" si je comprend bien (car on pose d/c environ égal à 0)
J'ai raisonne effectivement en prenant d 30m comme c'est le cas sur un terrain de foot.
Mais si t2< d/c alors t'<0 , ceci est valable que soit la valeur de d
Donc tu peux peut être construire des cas relativistes où d est très grand et où t2 peut être alors non negligeable.
C'est plus vraiment un terrain de foot mais bon...
J'ai raisonne effectivement en prenant d
30m comme c'est le cas sur un terrain de foot.
Mais si t2<
d/c alors t'<0 , ceci est valable que soit la valeur de d
Ah oui effectivement ça marche aussi en fait, je n'avais pas bien vu ce détail. Bon je pense que je comprends assez pour commencer à rédiger quelque chose qui tient la route, je reviendrai si j'ai d'autres doutes j'espère que non !
Merci beaucoup pour ton aide krinn
De rien, c'était un exo qui m'a bien plu...
N'hésite pas à poster si tu as de nouveaux elements , on a peut être omis qqchose...
La relat' c'est piegeux
Re en fait maintenant je pense que au tout début quand j'ai calculé j'a pris des conditions bizarres donc ça me donnait un "forcément négatif" mais pas avec les "bonnes raisons"... je me cite :
Dans R je pose :
Mais en fait je prend comme état de fait que P va toucher la balle au même moment exact que D sera dépassé par A (en gros E_1 et E_2 simultanés dans R).... or je n'ai aucune raison de prendre ça, c'est totalement arbitraire
Et c'est sur ça que je me suis basé pour calculer après mon Oui , au début tu as eu une idée qui t'a permis d'avancer .
Mais ensuite on a raisonne sur un t2 quelconque.
Donc le resultat final est bon.
Et l'intervalle est bien negatif
Hmm... donc le raisonnement c'est de me mettre dans une configuration tout à fait "spéciale", qui va bien car j'ai les temps identiques, et calculer l'invariant comme ça; et je trouve son signe. Mais du coup comme l'invariant est un invariant, il aura le même signe après quelles que soient les configurations que je prenne, même si ces configurations sont différentes de cette configuration "spéciale". C'est bien ça ?
Non.
1) Tu as eu une intuition et tu as découvert que dans un cas particulier on avait un intervalle négatif entre E1 et E2, doNC on avait une chance de trouver des arbitres qui ne soient pas d'accord sur le hors jeu.
Jusque là, ça ne suffit pas pour répondre.
2) on a ensuite repris le pb de manière plus generale:
Prenons tjs R où P est fixe en x=0 et tape à t=0 la balle pour faire sa passe (Eb1)
Et R' lié à A, avec l'axe Ax' confondu avec Ox
On a alors:
E1(0,0) dans R
E1( x'1, t'1) dans R'
E2(d, t2) dans R
E2(x'2, t'2) dans R'
....
...
....
voir post du 27 /01 a 00:05
Et on trouve finalement avec la transfo. de Lorentz,
t2< d/c dans R si on veut t' <0 dans R'
Et alors, effectivement , on voit que
l'intervalle est bien négatif,
car |t2| < d/c puisque <1
Mais tu n'as qu'à reprendre la partie 2) pour rédiger ta solution, ton intuition initiale n'a pas besoin d'être mentionnée
Annuler
connectez vous