Inscription / Connexion Nouveau Sujet
Exo thermo pompe à chaleur
Bonjour, j'ai besoin d'aide pour un exercice sur une pompe à chaleur.
Voici l?énoncé:
On considère une pompe à chaleur (P.A.C.) servant au chauffage d?une habitation,
fonctionnant entre deux sources de chaleur, de températures TC = 330 K et TF = 280 K.
1) Faire un schéma symbolique donnant le principe thermodynamique de la P.A.C. en
précisant le sens des échanges d'énergie. Définir le coefficient d?efficacité ?, et établir, à partir
des deux principes son expression pour un fonctionnement réversible.
2) Par suite des irréversibilités, le coefficient d?efficacité réel est égal au coefficient maximal
multiplié par 0,4. La puissance reçue par la source chaude (circuit d?eau chaude de l?habitation)
de la P.A.C. est PC = 10 kW. On envisage d?utiliser comme source froide l?eau d?un étang de volume V = 600 m3 , dont la température au milieu de l?hiver est TF = 280 K. Cette eau est acheminée jusqu?à l?habitation où, dans un échangeur thermique adapté, elle cède de la chaleur au fluide de la P.A.C. L?eau sort de l?échangeur à la température TS = 276 K, puis elle est rejetée dans l?étang. On donne la masse volumique ? = 103 kg.m?3
, la capacité calorifique C = 4180 J.K?1kg?1 de l?eau et on prend g = 10 m.s?2
a) Calculer la puissance PF cédée par l?eau de l?étang à la P.A.C.
b) En déduire le débit volumique avec lequel il faut prélever l?eau dans l?étang.
c) Que vous inspirent les ordres de grandeur du problème pour une utilisation tout au
long de l?hiver ?
3) On envisage plutôt de prélever l?eau dans une nappe phréatique (de température TF)
située à la profondeur h = 25 m. On procède comme au §2 : on rejette l?eau dans la nappe
après passage dans l?échangeur et les valeurs numériques sont inchangées.
a) La puissance Phydro de la pompe hydraulique qui achemine l?eau de la nappe jusqu?à
l?habitation est Phydro = ?p.D avec ?p : différence de pression hydrostatique dans la colonne d?eau verticale. Calculer cette puissance.
b) En déduire la puissance totale nécessaire au fonctionnement de l?installation.
Pourquoi cette solution est-elle plus satisfaisante que celle du §2
Voici ce que j?ai fais question 1)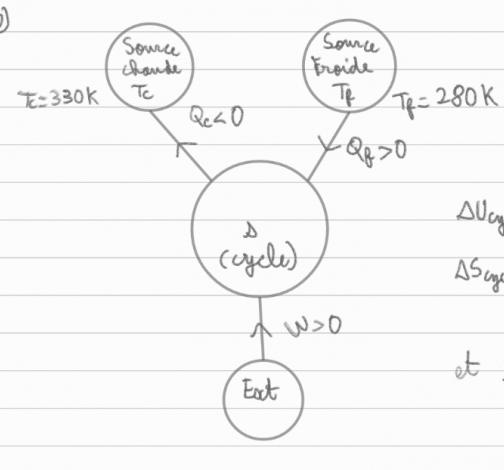
**image recadrée**les recherches doivent être recopiées**
Par contre pour la 2)a) je ne sais pas trop comment partir.
** image supprimée **
Merci de votre aide
* modération > Image effacée. Merci d'utiliser les outils mis à ta disposition pour écrire les formules mathématiques 
*
Bonsoir
Pour 2 : connais-tu le premier principe de la thermodynamique applicable aux systèmes ouverts ?
Pour la question 2)b)
J'ai utilisé le premier principles industrielle que j'ai appliqué à l'eau de l'étang.
Dmassique.
h=Pthermique=-QF/t
Avec Dmassique=
.D
Et h=C(Tc-TF)
Qui me donne
.D.C(Tc-TF)=P.(Tc+TF)/(Tc-TF)
Donc je trouve le débit volumique D en m3.s-1:
D=P.(Tc+TF)/.(Tc-TF)2.C
Mais je ne suis pas sure
Pas tout à fait d'accord avec ta prise en compte de l'irréversibilité. Je donne l'essentiel sans détailler les calculs.
Efficacité du cycle ditherme réversible :
Efficacité réelle du cycle :
Puissance thermique algébrique cédée à la source chaude : Pc=-104W
(il suffit de diviser par le temps t de fonctionnement numérateur et dénominateur)
Puissance mécanique :
L'énergie interne étant une fonction d'état, sur un cycle :
En notant Pf la puissance thermique reçue à la source froide et en divisant par t la relation précédente :
Tu devrais être capable de continuer maintenant.
Ok merci.
Par contre à quelle moment utilise-t-on le fait que l'eau sort de l'échangeur à la température Ts=276K.
Pour le débit volumique je trouve 4 litres par seconde en utilisant Ts.
Est-ce juste ?
Et pour la 2)c) je pense que au vu du volume de l'étang de seulement 600m3. La pompe à chaleur n'aura pas une très grande efficacité avec le temps
En supposant l'échangeur thermique parfait, la puissance thermique Pf reçue par le fluide circulant dans la pompe à chaleur est égale à la puissance thermique perdue par l'eau de l'étang :
Soit un débit volumique de l'eau de l'étang :
OK merci. Je m'étais trompé sur mes valeurs.
Du coup pour la 3)a)
J'utilise la relation dp/dz=-.g (z verticale ascendante) pour les fluides incompressibles dans le champ de pesanteur:
donc p=-.g.z+cste avec cste=105Pa
D'où p=.g.h+105 avec h=25 m
p=250000+100000=350000 Pa =3,5 bar
Or on sait que Phydro=p.Dv
Phydro=350000*3,71.10-4=92,75 kg.m2.s-3=92,75 W
pour la 3)b)
Je ne sais pas comment faire.
La puissance de la pompe est égale au produit du débit massique par la variation d'énergie potentielle massique de pesanteur : g.h. Il est facile de démontrer (ce n'est pas demandé ici) que cette puissance est aussi égale au produit du débit volumique par la variation de pression due à l'altitude µ.g.h représente environ 2,5bars et non 3,5bars. Ensuite, il suffit d'ajouter la puissance de la pompe hydraulique à la puissance mécanique de la pompe à chaleur Pm obtenue précédemment pour faire le bilan.
Tu peux généraliser le premier principe de la thermo à l'eau de la nappe phréatique. Son enthalpie massique ne varie pas mais son énergie potentielle augmente de la valeur nulle (altitude nulle choisie arbitrairement à la surface libre de la nappe) à la valeur g.h si h est l'augmentation d'altitude produite par la pompe hydraulique. Cela donne :
Puisque le débit volumique D de l'eau est relié au débit massique Dm par la relation :
(µ.g.h) représente la différence de pression entre l'eau au niveau du sol et l'eau à la profondeur h, pas la pression à la profondeur h.
Ah oui je comprends mieux merci.
Pour la 3)b)
J'ai fais Pm+Phydro=3,79.103+92,75
=3,88.103=-PC-PF
Or -PC=-104W
Donc PF=3,88.103+104=13,8 kW
Donc dans ce cas là, PF est deux fois plus grand que lorsque l'on prélève l'eau dans l'étang
Question 3b : la puissance coûteuse est :
Pc=Pm+Phydro=3,88kW
Mais le fonctionnement de la pompe est distinct du fonctionnement cyclique de la pompe à chaleur. Les valeurs de Pc et Pf obtenues aux questions précédentes restent identiques pour peu que Tc et Tf restent inchangées.
La puissance coûteuse correspond à l'énergie que l'on devra apporter à la pac pour la faire fonctionner ?
Mais ducoup je ne comprends pas pourquoi on nous dit dans l'énoncé que cette solution est plus satisfaisante que celle du paragraphe 2(question 2).
Là j'ai juste l'impression qu'on consomme plus d'énergie pour un rendement égale.
Est-ce lié au faite que l'eau du lac peut geler donc bloquer le fonctionnement de la pac alors que l'eau souterraine ne peut pas geler ?
Tu es sur la bonne voie...
La température de l'eau du lac peut varier. Prenons l'exemple d'un hiver rigoureux avec une température de l'air inférieure à 0°C. Une couche de glace va se former et, en imaginant le captage de l'eau à une certaine profondeur, l'eau captée va avoir une température proche de 0°C . Imaginons TF=274K plutôt que 280K ; L'efficacité du cycle réversible tombe à 5,89 et celle du cycle réel à 2,36. La pompe à chaleur est donc nettement moins économique.
En revanche, l'eau de la nappe phréatique garde une température pratiquement constante toute l'année. Ton énoncé la suppose égale à 7°C : c'est vraiment un cas extrême, choisi par l'énoncé pour ne pas avoir à refaire les calculs car les nappes phréatiques ont plutôt une température de l'ordre de 12°C toute l'année, ce qui porte l'efficacité du cycle réversible à 7,33 et l'efficacité réelle à 2,93. Cela compense largement le coût de fonctionnement de la pompe nécessaire à faire remonter l'eau de la nappe phréatique.
Annuler
connectez vous