Inscription / Connexion Nouveau Sujet
Exo d'hydrodynamique
Salut,
J'ai besoin d'aide pour la résolution de cet exercice:
Deux grands réservoirs ouverts à l'air libre A et F contiennent le même liquide. Un tuyau horizontal BCE, avec une section C plus étroite et une extrémité D à l'air libre, est attaché à la base du réservoir A. Un tube vertical E est relié à la section C et conduit le liquide au réservoir F. Le fluide n'est pas visqueux. Si la section du tube en C est la moitié de celle en S et si D est situé à une hauteur h1 sous le niveau du réservoir A, exprimer h2 en fonction de h1.
Solution: h2 = 3h1
- je sais que, vu que le liquide n'est pas visqueux, on peut utiliser l'équation de Bernoulli, mais j'arrive pas à comprendre comment est-ce qu'il faut faire pour arriver à résoudre l'éxo.
Merci d'avance! ^^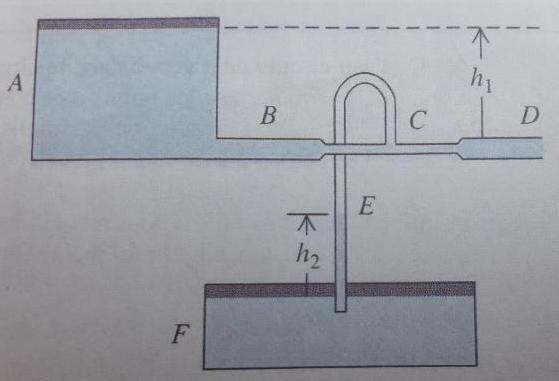
***Image recadrée***
Bonjour
1° : théorème de Bernouilli appliqué entre A et C
2° : théorème de Bernouilli appliqué entre C et D en tenant compte de la conservation du débit
3° : Relation de la statique des fluides appliquée entre E et la surface libre du récipient F donnant 
.g.h2 en fonction de (Patm -PE)=(Patm -PC). Les points C et E sont à la même pression et on peut considérer la surface libre du récipient A comme fixe puisque l'aire de cette surface libre est beaucoup plus grande que l'aire de la section droite du tube en C et en D...
Avec ces hypothèses simplificatrices, on obtient bien : h2=3h1
Bonjour, @vanoise
Pouvez vous donner plus d'informations sur la résolution de cette exercice ?
Merci beaucoup
Paulux9801, bonjour
peux-tu renseigner ton niveau d'études s'il te plaît dans ton profil ?
extrait de 
la FAQ du forum :Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau topic ?
équivalences des systèmes de niveaux scolaires
en outre, des indications ont déjà été données, mets les en oeuvre et propose quelque chose maintenant
Etape n° 1 : La variation de pression avec l'altitude dans l'air est négligeable : PC=PE : pression facile à exprimer en fonction de Patm et .g.h2
Etape n° 2 : appliquer le théorème de Bernouilli entre la surface libre de A, C et D en remarquant que la surface libre de A est quasi immobile et à la pression atmosphérique et en remarquant que la pression en D est aussi égale égale à la pression atmosphérique.
Etape n° 3 : trouver la relation simple entre les vitesses VC et VD en raisonnant sur la conservation du débit volumique.
Etape n° 4 : simplifier la relation 2 en tenant compte de la relation 3 conduit au résultat attendu.
Je te laisse réfléchir et proposer une solution. Pose si tu le juges utile des questions précises sur ce que tu ne comprends pas.
vanoise
Merci pour votre réponse.
Voici ce que j'ai fait mais je n'arrive pas à continuer.
Avec l'équation de continuité j'ai trouvé :
Vd = Vc/2
Ensuite, j'ai fait le théorème de Bernoulli entre À et C et je trouve : Pa + p.g.ha = Pc + 1/2.p.Vc^2 + p.g.hc
En sachant que Pa=Patm
J'ai refait le théorème de Bernoulli entre C et D et je trouve : Pc + 1/2.p.Vc^2 + p.g.hc = Pd + 1/2.p.Vd^2 + p.g.hd
En sachant que Pd = Patm
Et j'ai que Pc = Pe = p.g.h2
Je ne sais pas comment simplifier et quelle hauteur correspond à quoi dans mon théorème de Bernoulli.
Tu y es presque. Je traduis en équations mon message précédent.
Etape n° 1 : statique des fluides :
PC=Pa-.g.h2
Etape n° 2 : théorème de Bernoulli en prenant comme niveau d'altitude nulle celui de C et D :
PA+.g.h1=PC+½.VC2
PC+½.VC2=Pa+½.VD2
Etape n° 3 : comme tu l'as trouvé :
VC=2VD
En reportant dans les deux égalités de l'étape 2 les résultats des étapes 1 et 3, on tombe sur le résultat demandé...
Je suis désolée mais j'obtiens pas du tout la bonne réponse.. je ne comprends pas
J'obtiens du théorème de bernoulli entre A et C 
j'ai simplifié PA avec la pression atmosphérique) p.g.h1 = -p.g.h2 + 1/2.p.vc^2
Et du théorème de bernoulli entre C et D :
-p.g.h2 + 1/2.p.vc^2 = 1/8.p.vc^2
Dans l'application de la relation de Bernoulli entre A et C, un ”PA” a pris malencontreusement la place d'un Pa dans mon message précédent ... J'espère que cela ne t'a pas vraiment gêné. Relation de Bernoulli entre A et D :
Relation de Bernoulli entre A et C en tenant compte des étapes 1 et 3 :
En simplifiant et en tenant compte de la relation (1) :
Je te laisse finir !
Bonjour,
Pourriez vous m'expliquer pourquoi Pc = Pa -*g*h2 ?
Je ne comprend pas d'ou viens cette relation
Merci
La relation fondamentale de la statique des fluides appliquée à la colonne d'eau de hauteur h2 donne :
avec :
* PF : pression à la surface libre du réservoir F : (pression atmosphérique)
La relation fondamentale de la statique des fluides appliquée à l'air contenu dans le tube entre C et E s'écrit :
La masse volumique de l'air est environ 800 fois plus petite que celle de l'eau. On peut donc négliger la variation de pression entre E et C devant les autres variations de pression du problème. Je te laisse terminer...
Annuler
connectez vous