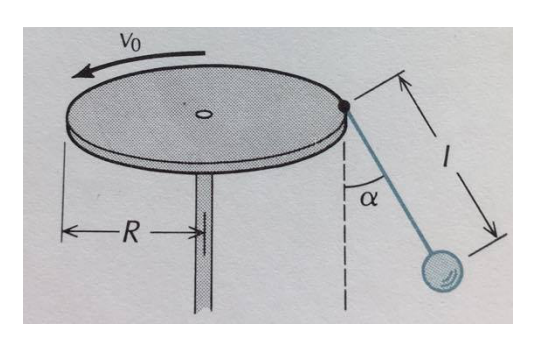
Bonjour
L' exercice est très proche du précédent. Si tu travailles dans un repère terrestre considéré comme galiléen, tu peux écrire que la petite boule est animée d'un mouvement circulaire uniforme autour de l'axe vertical matérialisé par l'axe du disque à une vitesse angulaire qui s'exprime facilement en fonction de R et V_o.
Le rayon de la trajectoire du centre de la boule, qui peut être noté "r" s'exprime facilement en fonction de R, l et . Tu peux ainsi facilement établir l'expression de l'accélération normale centripète de vecteur a_n.
La boule est soumise à l'action de deux forces comme dans l'autre exercice :
- son poids de vecteur P ;
- l'action du fil de vecteur N colinéaire au fil...
Je te laisse continuer... N'oublie pas de compléter le schéma, cela est nécessaire pour bien projeter les vecteurs sur deux axes.

J'ai essayé d'appliquer le pfd avec le poids P et la tension du fil T et avec l'accélération centripète a=v²/r.
Et finalement je trouve une expression de la sorte : v=RACINE(g*tan(a)*(R+l*sin(a)))
Je ne sais pas si l'expression de v est juste.

Si je comprends bien l'énoncé, il s'agit de déterminer la vitesse notée V_o sur le schéma ; il s'agit de la vitesse d'un point à la périphérie du disque de rayon R et non de la vitesse v du centre de la boule. Avec la définition de "r" déjà donnée, il est préférable d'écrire l'expression de l'accélération normale centripète sous la forme :
a_n=r.² avec :


Je te laisse corriger...

Ah d'accord.
Donc si j'ai bien compris, vo = RACINE(g*tan(a)/r) * R ?

Ton dernier résultat est correct. Il convient cependant de remplacer r par son expression :
r=R+l.sin() , ce qui donne au final :

Merci pour votre aide!